
【题目】如图,直线y=mx+n与双曲线y=![]() 相交于A(﹣1,2)、B(2,b)两点,与y轴相交于点C.
相交于A(﹣1,2)、B(2,b)两点,与y轴相交于点C.
(1)求m,n的值;
(2)若点D与点C关于x轴对称,求△ABD的面积;
(3)在坐标轴上是否存在异于D点的点P,使得S△PAB=S△DAB?若存在,直接写出P点坐标;若不存在,说明理由。
【答案】(1)m=﹣1,n=1;(2)3;(3)存在,P点坐标为(﹣1,0)或(3,0)或(0,3)
【解析】
(1)首先根据点A的坐标求出反比例函数的解析式,进而得出点B坐标,然后用待定系数法即可得出m,n的值;
(2)分别求出点C、D的坐标,即可求出△ABD的面积;
(3)分类求解,当点P在x轴上和y轴上时,即可得解.
(1)∵点A(﹣1,2)在双曲线y=![]() 上,
上,
∴2=![]() ,
,
解得,k=﹣2,
∴反比例函数解析式为:y=﹣![]() ,
,
∴b=![]() =﹣1,
=﹣1,
则点B的坐标为(2,﹣1),
∴![]() ,
,
解得,m=﹣1,n=1;
(2)由(1)知y=﹣x+1,当x=0时,y=1,
∴点C的坐标为(0,1),
∵点D与点C关于x轴对称,
∴点D的坐标为(0,﹣1),
∴△ABD的面积=![]() ×2×3=3;
×2×3=3;
(3)对于y=﹣x+1,当y=0时,x=1,
∴直线y=﹣x+1与x轴的交点坐标为(1,0),
当点P在x轴上时,设点P的坐标为(![]() ,0),
,0),
S△PAB=![]() ×|1﹣
×|1﹣![]() |×2+
|×2+![]() ×|1﹣
×|1﹣![]() |×1=3,
|×1=3,
解得,![]() =﹣1或3,
=﹣1或3,
∴P点坐标为(-1,0)或(3,0),
当点P在y轴上时,设点P的坐标为(0,b),
S△PAB=![]() ×|1﹣b|×2+
×|1﹣b|×2+![]() ×|1﹣b|×1=3,
×|1﹣b|×1=3,
解得,b=﹣1或3,
∴P点坐标为(0,-1)或(0,3),
又∵点P异于D点,D(0,-1),
∴P(0,3),
综上,P点坐标为(﹣1,0)或(3,0)或(0,3).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
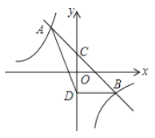
【题目】中国科学技术馆有“圆与非圆”展品,涉及了“等宽曲线”的知识.因为圆的任何一对平行切线的距离总是相等的,所以圆是“等宽曲线”.除了例以外,还有一些几何图形也是“等宽曲线”,如勒洛只角形(图1),它是分别以等边三角形的征个顶点为圆心,以边长为半径,在另两个顶点间画一段圆弧.三段圆弧围成的曲边三角形.图2是等宽的勒洛三角形和圆.
下列说法中错误的是( )
A.勒洛三角形是轴对称图形
B.图1中,点A到![]() 上任意一点的距离都相等
上任意一点的距离都相等
C.图2中,勒洛三角形上任意一点到等边三角形DEF的中心![]() 的距离都相等
的距离都相等
D.图2中,勒洛三角形的周长与圆的周长相等
查看答案和解析>>
科目:初中数学 来源: 题型:
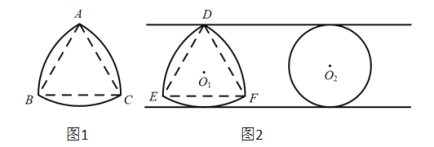
【题目】如图,已知正方形![]() 的边长为4,
的边长为4,![]() 是边
是边![]() 上的一个动点,连接
上的一个动点,连接![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,顶点
,顶点![]() 在线段
在线段![]() 上,对角线
上,对角线![]() ,
,![]() 相交于点
相交于点![]() .
.

(1)若![]() ,则
,则![]() ;
;
(2)①求证:点![]() 一定在
一定在![]() 的外接圆上;
的外接圆上;
②当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,点
时,点![]() 也随之运动,求点
也随之运动,求点![]() 经过的路径长;
经过的路径长;
(3)在点![]() 从点
从点![]() 到点
到点![]() 的运动过程中,
的运动过程中,![]() 的外接圆的圆心也随之运动,求该圆心到边
的外接圆的圆心也随之运动,求该圆心到边![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是根据某市2010年至2014年工业生产总值绘制的折线统计图,观察统计图获得以下信息,其中信息判断错误的是( )

A.2010年至2014年间工业生产总值逐年增加
B.2014年的工业生产总值比前一年增加了40亿元
C.2012年与2013年每一年与前一年比,其增长额相同
D.从2011年至2014年,每一年与前一年比,2014年的增长率最大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区在距离地面![]() 米的悬崖点
米的悬崖点![]() 处垂直水平线搭建了一个悬崖秋千,秋千拉绳均由钢管制作而成,当游客乘坐该秋千时,机器会将秋千拉至最高接近与地面平行的点
处垂直水平线搭建了一个悬崖秋千,秋千拉绳均由钢管制作而成,当游客乘坐该秋千时,机器会将秋千拉至最高接近与地面平行的点![]() 处(此时
处(此时![]() ) ,然后放下.该悬崖秋千以其惊险刺激立即成为网红打卡地.
) ,然后放下.该悬崖秋千以其惊险刺激立即成为网红打卡地.
![]() 若秋千放下
若秋千放下![]() 秒后
秒后![]() 点
点![]() 的垂直距离为
的垂直距离为![]() 米,求秋千拉绳
米,求秋千拉绳![]() 的长;
的长;
![]() 若某一时刻秋千荡至与点
若某一时刻秋千荡至与点![]() 水平距离相距
水平距离相距![]() 米的点
米的点![]() 处,求
处,求![]() 的度数,并求此时秋千底端距离悬崖底部多少米(结果保留整数参考数据:
的度数,并求此时秋千底端距离悬崖底部多少米(结果保留整数参考数据:![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
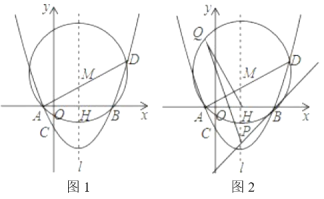
【题目】如图1,在平面直角坐标系中,抛物线y![]() x2bxc交x轴于点A,B,点B的坐标为(4,0),与y轴于交于点C(0,﹣2).
x2bxc交x轴于点A,B,点B的坐标为(4,0),与y轴于交于点C(0,﹣2).
(1)求此抛物线的解析式;
(2)在抛物线上取点D,若点D的横坐标为5,求点D的坐标及∠ADB的度数;
(3)在(2)的条件下,设抛物线对称轴![]() 交x轴于点H,△ABD的外接圆圆心为M(如图1),
交x轴于点H,△ABD的外接圆圆心为M(如图1),
①求点M的坐标及⊙M的半径;
②过点B作⊙M的切线交![]() 于点P(如图2),设Q为⊙M上一动点,则在点Q运动过程中
于点P(如图2),设Q为⊙M上一动点,则在点Q运动过程中![]() 的值是否变化?若不变,求出其值;若变化,请说明理由.
的值是否变化?若不变,求出其值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
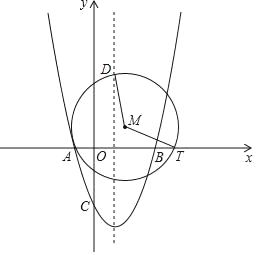
【题目】如图,二次函数y=x2+bx﹣3的图象与x轴分别相交于A、B两点,点B的坐标为(3,0),与y轴的交点为C,动点T在射线AB上运动,在抛物线的对称轴l上有一定点D,其纵坐标为2![]() ,l与x轴的交点为E,经过A、T、D三点作⊙M.
,l与x轴的交点为E,经过A、T、D三点作⊙M.
(1)求二次函数的表达式;
(2)在点T的运动过程中,
①∠DMT的度数是否为定值?若是,请求出该定值:若不是,请说明理由;
②若MT=![]() AD,求点M的坐标;
AD,求点M的坐标;
(3)当动点T在射线EB上运动时,过点M作MH⊥x轴于点H,设HT=a,当OH≤x≤OT时,求y的最大值与最小值(用含a的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点A和点B(3,0),与
轴交于点A和点B(3,0),与![]() 轴交于点C(0,3).
轴交于点C(0,3).
(1)求抛物线的解析式;
(2)若点M是抛物线在![]() 轴下方上的动点,过点M作MN//
轴下方上的动点,过点M作MN//![]() 轴交直线BC于点N,求线段MN的最大值;
轴交直线BC于点N,求线段MN的最大值;
(3)在(2)的条件下,当MN取最大值时,在抛物线的对称轴![]() 上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com