
【题目】如图,已知正方形![]() 的边长为4,
的边长为4,![]() 是边
是边![]() 上的一个动点,连接
上的一个动点,连接![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,顶点
,顶点![]() 在线段
在线段![]() 上,对角线
上,对角线![]() ,
,![]() 相交于点
相交于点![]() .
.
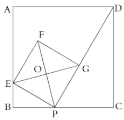

(1)若![]() ,则
,则![]() ;
;
(2)①求证:点![]() 一定在
一定在![]() 的外接圆上;
的外接圆上;
②当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,点
时,点![]() 也随之运动,求点
也随之运动,求点![]() 经过的路径长;
经过的路径长;
(3)在点![]() 从点
从点![]() 到点
到点![]() 的运动过程中,
的运动过程中,![]() 的外接圆的圆心也随之运动,求该圆心到边
的外接圆的圆心也随之运动,求该圆心到边![]() 的距离的最大值.
的距离的最大值.
【答案】(1)![]() ;(2)①详见解析;②2
;(2)①详见解析;②2![]() ;(3)
;(3)![]()
【解析】
(1)由正方形的性质得出∠C=∠B=∠EPG=90°,PF⊥EG,CD=BC=4,∠OEP=45°,由角的互余关系证出∠BEP=∠DPC,得出△CDP∽△BPE,得出对应边成比例即可求出BE的长;
(2)①B、P、O、E四点共圆,即可得出结论;
②连接BO、BD,由勾股定理求出BD=4![]() ,由圆周角定理得出∠OBP=∠OEP=45°,周长点O在BD上,当P运动到点C时,O为BD的中点,即可得出答案;
,由圆周角定理得出∠OBP=∠OEP=45°,周长点O在BD上,当P运动到点C时,O为BD的中点,即可得出答案;
(3)设![]() 的外接圆的圆心为M,作MN⊥CB于N,由三角形中位线定理得出MN=
的外接圆的圆心为M,作MN⊥CB于N,由三角形中位线定理得出MN=![]() BE,设BP=x,则CP=4-x,由相似三角形的对应边成比例求出BE=x-
BE,设BP=x,则CP=4-x,由相似三角形的对应边成比例求出BE=x-![]() x2=-
x2=-![]() (x-2)2+1,由二次函数的最大值求出BE的最大值为1,得出MN的最大值=
(x-2)2+1,由二次函数的最大值求出BE的最大值为1,得出MN的最大值=![]() 即可.
即可.
解:(1)∵四边形ABCD、四边形PEFG是正方形,
∴∠C=∠B=∠EPG=90°,PF⊥EG,CD=BC=4,∠OEP=45°,
∴∠BEP+∠BPE=90°,∠DPC+∠BPE=90°,
∴∠BEP=∠DPC,
∴△CDP∽△BPE;
∴![]() ,即
,即![]()
∴BE=![]()
(2)①证明:如图,
取PE的中点Q,连接BQ,OQ,
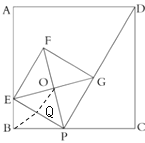
∵∠POE=90°,
∴OQ=![]() PE,
PE,
∵△BPE是直角三角形,
∴点Q是Rt△BPE外接圆的圆心,
∴BQ=![]() PE,
PE,
∴OQ=BQ,
∴点O一定在△APE的外接圆上;(到圆心的距离等于半径的点必在此圆上)
②解:连接OB、BD,如图所示:
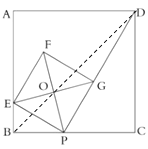
∵四边形ABCD是正方形,
∴∠ABC=90°,∠DBC=45°,
∴BD=![]() =4
=4![]() ,
,
∵B、P、O、E四点共圆,
∴∠OBP=∠OEP=45°,
∴点O在BD上,
当P运动到点C时,O为BD的中点,OB=![]() BD=2
BD=2![]() ,
,
即点O经过的路径长为2![]() ;
;
(3)解:设△BPE的外接圆的圆心为M,作MN⊥BC于N,如图:
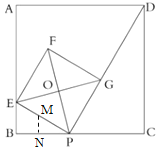
则MN∥BE,
∵ME=MP,
∴BN=PN,
∴MN=![]() BE,
BE,
设BP=x,则PC=4-x,
由(1)得:△CDP∽△BPE,
∴![]() ,即
,即![]() ,
,
解得:BE=x-![]() x2=-
x2=-![]() (x-2)2+1
(x-2)2+1
∴x=2时,BE的最大值为1,此时MN的值最大=![]() ,
,
即△APE的圆心到BC边的距离的最大值为![]() .
.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案科目:初中数学 来源: 题型:
【题目】定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°.
①若AB=CD=1,AB∥CD,求对角线BD的长.
②若AC⊥BD,求证:AD=CD;
(2)如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
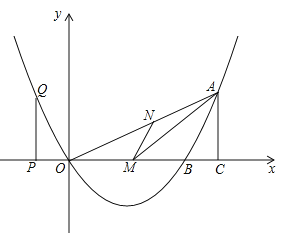
【题目】如图,已知二次函数的图象过点![]() .
.![]() ,与
,与![]() 轴交于另一点
轴交于另一点![]() ,且对称轴是直线
,且对称轴是直线![]() .
.
(1)求该二次函数的解析式;
(2)若![]() 是
是![]() 上的一点,作
上的一点,作![]() 交
交![]() 于
于![]() ,当
,当![]() 面积最大时,求
面积最大时,求![]() 的长;
的长;
(3)![]() 是
是![]() 轴上的点,过
轴上的点,过![]() 作
作![]() 轴与抛物线交于
轴与抛物线交于![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() ,当以
,当以![]() 为顶点的三角形与以
为顶点的三角形与以![]() 为顶点的三角形相似时,求
为顶点的三角形相似时,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017江西省)如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直.
(1)若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;
(2)若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°?
(参考数据:sin69°≈![]() ,cos21°≈
,cos21°≈![]() ,tan20°≈
,tan20°≈![]() ,tan43°≈
,tan43°≈![]() ,所有结果精确到个位)
,所有结果精确到个位)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售部为了调动销售员的积极性,决定实行目标管理,根据目标完成的情况对销售员进行适当的奖励.为了确定一个适当的月销售目标,该公司统计了销售部每位销售员在某月的销售额(单位:万元),并将结果绘制成如图所示的统计图.
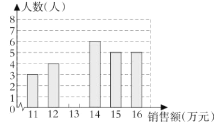
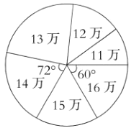
图1 图2
(1)补全如图1所示的统计图;
(2)月销售额在 万元的人数最多,该公司销售部人均月销售额是 万元;
(3)若想让一半左右的销售员都能达到销售目标,你认为月销售额定为多少合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
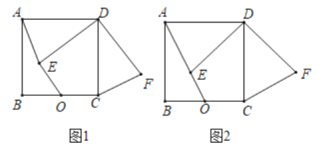
【题目】如图,正方形![]() 中,
中,![]() ,
,![]() 是
是![]() 边的中点,点
边的中点,点![]() 是正方形内一动点,
是正方形内一动点,![]() ,连接
,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得
得![]() ,连接
,连接![]() ,
,![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图2,若![]() ,
,![]() ,
,![]() 三点共线,求点
三点共线,求点![]() 到直线
到直线![]() 的距离.
的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=mx+n与双曲线y=![]() 相交于A(﹣1,2)、B(2,b)两点,与y轴相交于点C.
相交于A(﹣1,2)、B(2,b)两点,与y轴相交于点C.
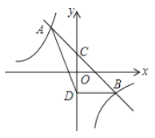
(1)求m,n的值;
(2)若点D与点C关于x轴对称,求△ABD的面积;
(3)在坐标轴上是否存在异于D点的点P,使得S△PAB=S△DAB?若存在,直接写出P点坐标;若不存在,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
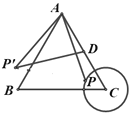
【题目】如图,等边三角形ABC中,AB=4cm,以C为圆心,1cm长为半径画⊙C,点P在⊙C上运动,连接AP,并将AP绕点A顺时针旋转60°至AP′,点D是边AC的中点,连接DP′.在点P移动的过程中,线段DP′长度的最小值为______cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
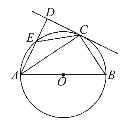
【题目】如图,已知AB是☉O的直径,DC是☉O的切线,点C是切点,AD⊥DC,垂足为D,且与圆O相交于点E.
(1)求证:∠DAC=∠BAC.
(2)若☉O的直径为5cm,EC=3cm,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com