
【题目】某公司销售部为了调动销售员的积极性,决定实行目标管理,根据目标完成的情况对销售员进行适当的奖励.为了确定一个适当的月销售目标,该公司统计了销售部每位销售员在某月的销售额(单位:万元),并将结果绘制成如图所示的统计图.
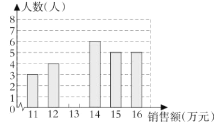
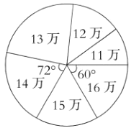
图1 图2
(1)补全如图1所示的统计图;
(2)月销售额在 万元的人数最多,该公司销售部人均月销售额是 万元;
(3)若想让一半左右的销售员都能达到销售目标,你认为月销售额定为多少合适?
【答案】(1)详见解析;(2)13;13.7;(3)想让一半左右的销售员都能达到销售目标,月销售额定为14万元合适.
【解析】
(1)结合条形图和扇形图得出样本容量,再得到13万对应的人数,从而画出条形图;
(2)根据条形图得到人数最多的销售额,再根据加权平均数公式计算加权平均数即可;
(3)由条形图得到中位数问题可解.
解:(1)销售人员总数为:![]() 人
人
则月销售额为13万的人数为:30-3-4-6-5-5=7人
画条形图如图;
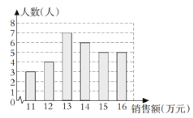
(2)由条形图可知,月销售额在13万元的人数最多;该公司销售部人均月销售额是![]() 万元 ;
万元 ;
故答案为13;13.7;
(3)由条形图可知,数据的中位数为14万元,因此,想让一半左右的销售员都能达到销售目标,月销售额定为14万元合适.


科目:初中数学 来源: 题型:
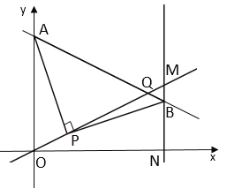
【题目】如图,平面直角坐标系中,已知直线![]() 经过点P(2,1),点A在y轴的正半轴上,连接PA,将线段PA绕点P顺时针旋转90°至线段PB,过点B作直线MN⊥x轴,垂足为N,交直线y=kx(k≠0)于点M(点M在点B的上方),且BN=3BM,连接AB,直线AB与直线
经过点P(2,1),点A在y轴的正半轴上,连接PA,将线段PA绕点P顺时针旋转90°至线段PB,过点B作直线MN⊥x轴,垂足为N,交直线y=kx(k≠0)于点M(点M在点B的上方),且BN=3BM,连接AB,直线AB与直线![]() 交于点Q,则点Q的坐标为__________.
交于点Q,则点Q的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在参加了市教育质量综合评价学业素养测试后,随机抽取八年级部分学生,针对发展水平四个维度“阅读素养、数学素养、科学素养、人文素养”,开展了“你最需要提升的学业素养”问卷调查(每名学生必选且只能选择一项).小明、小颖和小雯在协助老师进行统计后,有这样一段对话:
小明:“选科学素养和人文素养的同学分别为16人,12人.”
小颖:“选数学素养的同学比选阅读素养的同学少4人.”
小雯:“选科学素养的同学占样本总数的20%.”
(1)这次抽样调查了多少名学生?
(2)样本总数中,选“阅读素养”、“数学素养”的学生各多少人?
(3)该校八年级有学生400人,请根据调查结果估计全年级选择“阅读素养”的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正六边形ABCDEF的对称中心P在反比例函数![]() 的图象上,边CD在x轴上,点B在y轴上.已知
的图象上,边CD在x轴上,点B在y轴上.已知![]() .
.
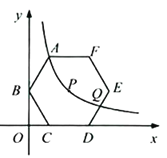
(1)点A是否在该反比例函数的图象上?请说明理由.
(2)若该反比例函数图象与DE交于点Q,求点Q的横坐标.
(3)平移正六边形ABCDEF,使其一边的两个端点恰好都落在该反比例函数的图象上,试描述平移过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形![]() 的边长为4,
的边长为4,![]() 是边
是边![]() 上的一个动点,连接
上的一个动点,连接![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,顶点
,顶点![]() 在线段
在线段![]() 上,对角线
上,对角线![]() ,
,![]() 相交于点
相交于点![]() .
.
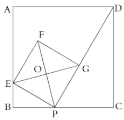

(1)若![]() ,则
,则![]() ;
;
(2)①求证:点![]() 一定在
一定在![]() 的外接圆上;
的外接圆上;
②当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,点
时,点![]() 也随之运动,求点
也随之运动,求点![]() 经过的路径长;
经过的路径长;
(3)在点![]() 从点
从点![]() 到点
到点![]() 的运动过程中,
的运动过程中,![]() 的外接圆的圆心也随之运动,求该圆心到边
的外接圆的圆心也随之运动,求该圆心到边![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是根据某市2010年至2014年工业生产总值绘制的折线统计图,观察统计图获得以下信息,其中信息判断错误的是( )

A.2010年至2014年间工业生产总值逐年增加
B.2014年的工业生产总值比前一年增加了40亿元
C.2012年与2013年每一年与前一年比,其增长额相同
D.从2011年至2014年,每一年与前一年比,2014年的增长率最大
查看答案和解析>>
科目:初中数学 来源: 题型:
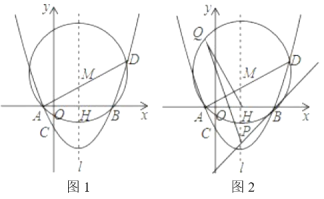
【题目】如图1,在平面直角坐标系中,抛物线y![]() x2bxc交x轴于点A,B,点B的坐标为(4,0),与y轴于交于点C(0,﹣2).
x2bxc交x轴于点A,B,点B的坐标为(4,0),与y轴于交于点C(0,﹣2).
(1)求此抛物线的解析式;
(2)在抛物线上取点D,若点D的横坐标为5,求点D的坐标及∠ADB的度数;
(3)在(2)的条件下,设抛物线对称轴![]() 交x轴于点H,△ABD的外接圆圆心为M(如图1),
交x轴于点H,△ABD的外接圆圆心为M(如图1),
①求点M的坐标及⊙M的半径;
②过点B作⊙M的切线交![]() 于点P(如图2),设Q为⊙M上一动点,则在点Q运动过程中
于点P(如图2),设Q为⊙M上一动点,则在点Q运动过程中![]() 的值是否变化?若不变,求出其值;若变化,请说明理由.
的值是否变化?若不变,求出其值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接:“国家卫生城市”复检,某市环卫局准备购买A,B两种型号的垃圾箱,通过市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需540元,购买2个A型垃圾箱比购买3个B型垃圾箱少用160元.
(1)求每个A型垃圾箱和B型垃圾箱各多少元?
(2)该市现需要购买A,B两种型号的垃圾箱共30个,其中买A型垃圾箱不超过16个.
①求购买垃圾箱的总花费w(元)与A型垃圾箱x(个)之间的函数关系式;
②当买A型垃圾箱多少个时总费用最少,最少费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com