
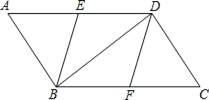
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy![]() x2bxcНЛxжсгкЕуAЃЌBЃЌЕуBЕФзјБъЮЊ(4ЃЌ0)ЃЌгыyжсгкНЛгкЕуC(0ЃЌЉ2)ЃЎ
x2bxcНЛxжсгкЕуAЃЌBЃЌЕуBЕФзјБъЮЊ(4ЃЌ0)ЃЌгыyжсгкНЛгкЕуC(0ЃЌЉ2)ЃЎ
ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкХзЮяЯпЩЯШЁЕуDЃЌШєЕуDЕФКсзјБъЮЊ5ЃЌЧѓЕуDЕФзјБъМАЁЯADBЕФЖШЪ§ЃЛ
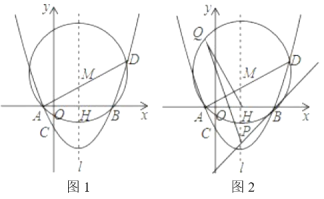
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЩшХзЮяЯпЖдГЦжс![]() НЛxжсгкЕуHЃЌЁїABDЕФЭтНгдВдВаФЮЊMЃЈШчЭМ1ЃЉЃЌ
НЛxжсгкЕуHЃЌЁїABDЕФЭтНгдВдВаФЮЊMЃЈШчЭМ1ЃЉЃЌ
ЂйЧѓЕуMЕФзјБъМАЁбMЕФАыОЖЃЛ
ЂкЙ§ЕуBзїЁбMЕФЧаЯпНЛ![]() гкЕуPЃЈШчЭМ2ЃЉЃЌЩшQЮЊЁбMЩЯвЛЖЏЕуЃЌдђдкЕуQдЫЖЏЙ§ГЬжа
гкЕуPЃЈШчЭМ2ЃЉЃЌЩшQЮЊЁбMЩЯвЛЖЏЕуЃЌдђдкЕуQдЫЖЏЙ§ГЬжа![]() ЕФжЕЪЧЗёБфЛЏЃПШєВЛБфЃЌЧѓГіЦфжЕЃЛШєБфЛЏЃЌЧыЫЕУїРэгЩЃЎ
ЕФжЕЪЧЗёБфЛЏЃПШєВЛБфЃЌЧѓГіЦфжЕЃЛШєБфЛЏЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉЕу
ЃЛЃЈ2ЃЉЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌ45ЁуЃЛЃЈ3ЃЉЂйЕу
ЃЌ45ЁуЃЛЃЈ3ЃЉЂйЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌ
ЃЌ![]() ЕФАыОЖЮЊ
ЕФАыОЖЮЊ![]() ЃЛЂкдкЕу
ЃЛЂкдкЕу![]() дЫЖЏЙ§ГЬжа
дЫЖЏЙ§ГЬжа![]() ЕФжЕВЛБфЃЌЦфжЕЮЊ
ЕФжЕВЛБфЃЌЦфжЕЮЊ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉНЋ![]() ЃЌ
ЃЌ![]() ДњШыНтЮіЪНЃЌЧѓГіНтЮіЪНЕФЯЕЪ§ЃЌМДПЩЕУНтЃЛ
ДњШыНтЮіЪНЃЌЧѓГіНтЮіЪНЕФЯЕЪ§ЃЌМДПЩЕУНтЃЛ
ЃЈ2ЃЉНЋ![]() ДњШыНтЮіЪНЃЌЧѓГі
ДњШыНтЮіЪНЃЌЧѓГі![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЕузјБъЃЛСю
ЕузјБъЃЛСю![]() ЃЌЧѓГіAЁЂBзјБъЃЌгЩЙДЙЩЖЈРэЛђСНЕуМфОрРыЙЋЪНЧѓГіADЁЂBDЃЌдйгЩУцЛ§ЗЈЧѓГіBHЃЌДгЖјЧѓГіЁЯADBЕФе§ЯвжЕЃЌПЩжЊЁЯADBЕФЖШЪ§ЃЛ
ЃЌЧѓГіAЁЂBзјБъЃЌгЩЙДЙЩЖЈРэЛђСНЕуМфОрРыЙЋЪНЧѓГіADЁЂBDЃЌдйгЩУцЛ§ЗЈЧѓГіBHЃЌДгЖјЧѓГіЁЯADBЕФе§ЯвжЕЃЌПЩжЊЁЯADBЕФЖШЪ§ЃЛ
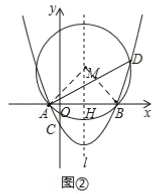
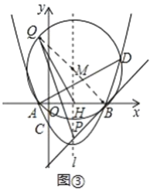
ЃЈ3ЃЉЂйгЩдВжмНЧЖЈРэНсКЯЕШбќжБНЧШ§НЧаЮБпЕФЙиЯЕЧѓГіЕу![]() ЕФзјБъКЭЁб
ЕФзјБъКЭЁб![]() ЕФАыОЖЃЛЂкжЄУїQHКЭQPЫљдкЕФЁїHMQКЭЁїQMPЯрЫЦМДПЩЃЎ
ЕФАыОЖЃЛЂкжЄУїQHКЭQPЫљдкЕФЁїHMQКЭЁїQMPЯрЫЦМДПЩЃЎ
ЃЈ1ЃЉНЋ![]() ЃЌ
ЃЌ![]() ДњШыНтЮіЪНЕУЃЌ
ДњШыНтЮіЪНЕУЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁрЩшХзЮяЯпЕФНтЮіЪНЮЊЃК![]()
ЃЈ2ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
ЁрЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() Лђ4ЃЌ
Лђ4ЃЌ
Ёр![]() ЃЌ
ЃЌ![]()
ШчЭМЃЌСЌНс![]() ЃЌзї
ЃЌзї![]() гк
гк![]() ЃЌ
ЃЌ

Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЂйШчЭМЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЁб
ЃЌЁб![]() ЕФАыОЖЮЊ
ЕФАыОЖЮЊ![]() ЃЛ
ЃЛ
ЂкШчЭМЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁпЙ§Еу![]() зїЁб
зїЁб![]() ЕФЧаЯпНЛ
ЕФЧаЯпНЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп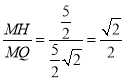 ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() Ёз
Ёз![]() ЃЌ
ЃЌ
Ёр ЃЌ
ЃЌ
ЁрдкЕу![]() дЫЖЏЙ§ГЬжа
дЫЖЏЙ§ГЬжа![]() ЕФжЕВЛБфЃЌЦфжЕЮЊ
ЕФжЕВЛБфЃЌЦфжЕЮЊ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌЕуEЁЂFЗжБ№ЪЧADЁЂBCЕФжаЕуЃЌЗжБ№СЌНгBEЁЂDFЁЂBDЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїAEBЁеЁїCFDЃЛ
ЃЈ2ЃЉШєЫФБпаЮEBFDЪЧСтаЮЃЌЧѓЁЯABDЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОЯњЪлВПЮЊСЫЕїЖЏЯњЪлдБЕФЛ§МЋадЃЌОіЖЈЪЕааФПБъЙмРэЃЌИљОнФПБъЭъГЩЕФЧщПіЖдЯњЪлдБНјааЪЪЕБЕФНБРј.ЮЊСЫШЗЖЈвЛИіЪЪЕБЕФдТЯњЪлФПБъЃЌИУЙЋЫОЭГМЦСЫЯњЪлВПУПЮЛЯњЪлдБдкФГдТЕФЯњЪлЖюЃЈЕЅЮЛЃКЭђдЊЃЉЃЌВЂНЋНсЙћЛцжЦГЩШчЭМЫљЪОЕФЭГМЦЭМ.
ЭМ1 ЭМ2
ЃЈ1ЃЉВЙШЋШчЭМ1ЫљЪОЕФЭГМЦЭМЃЛ
ЃЈ2ЃЉдТЯњЪлЖюдк ЭђдЊЕФШЫЪ§зюЖрЃЌИУЙЋЫОЯњЪлВПШЫОљдТЯњЪлЖюЪЧ ЭђдЊЃЛ
ЃЈ3ЃЉШєЯыШУвЛАызѓгвЕФЯњЪлдБЖМФмДяЕНЯњЪлФПБъЃЌФуШЯЮЊдТЯњЪлЖюЖЈЮЊЖрЩйКЯЪЪЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпy=mx+nгыЫЋЧњЯпy=![]() ЯрНЛгкAЃЈЉ1ЃЌ2ЃЉЁЂBЃЈ2ЃЌbЃЉСНЕуЃЌгыyжсЯрНЛгкЕуCЃЎ
ЯрНЛгкAЃЈЉ1ЃЌ2ЃЉЁЂBЃЈ2ЃЌbЃЉСНЕуЃЌгыyжсЯрНЛгкЕуCЃЎ
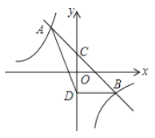
ЃЈ1ЃЉЧѓmЃЌnЕФжЕЃЛ
ЃЈ2ЃЉШєЕуDгыЕуCЙигкxжсЖдГЦЃЌЧѓЁїABDЕФУцЛ§ЃЛ
ЃЈ3ЃЉдкзјБъжсЩЯЪЧЗёДцдквьгкDЕуЕФЕуPЃЌЪЙЕУSЁїPAB=SЁїDABЃПШєДцдкЃЌжБНгаДГіPЕузјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌаЁУїгУЭМаЮМЦЫуЦїЛцжЦСЫШчЭМЫљЪОЕФЙигк![]() жсЖдГЦЕФЭМаЮЃЌИУЭМаЮгЩзѓгвСНВрЕФСНЖЮЗДБШР§КЏЪ§ЭМЯѓКЭ
жсЖдГЦЕФЭМаЮЃЌИУЭМаЮгЩзѓгвСНВрЕФСНЖЮЗДБШР§КЏЪ§ЭМЯѓКЭ![]() ЙЙГЩЃЌЕу
ЙЙГЩЃЌЕу![]() ЧЁЮЊ
ЧЁЮЊ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЃЎ
ЃЎ
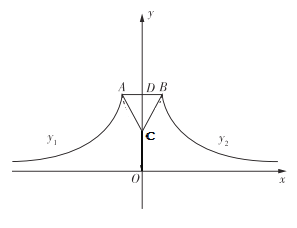
![]() ЧѓзѓгвСНВрЗДБШР§КЏЪ§ЕФЙиЯЕЪН(вЊЧѓЗжБ№зЂУїздБфСПЕФШЁжЕЗЖЮЇ)ЃЛ
ЧѓзѓгвСНВрЗДБШР§КЏЪ§ЕФЙиЯЕЪН(вЊЧѓЗжБ№зЂУїздБфСПЕФШЁжЕЗЖЮЇ)ЃЛ
![]() ЦНаагк
ЦНаагк![]() жсЕФжБЯп
жсЕФжБЯп![]() гыИУЭМаЮгаШ§ИіНЛЕуЃЌЧыЧѓГіНЛЕузјБъЃЛ
гыИУЭМаЮгаШ§ИіНЛЕуЃЌЧыЧѓГіНЛЕузјБъЃЛ
![]() ЧыЗжБ№аДГіжБЯп
ЧыЗжБ№аДГіжБЯп![]() гыИУЭМаЮгаСНИіНЛЕуКЭУЛгаНЛЕуЪБ
гыИУЭМаЮгаСНИіНЛЕуКЭУЛгаНЛЕуЪБ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
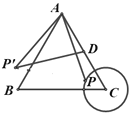
ЁОЬтФПЁПШчЭМЃЌЕШБпШ§НЧаЮABCжаЃЌAB=4cmЃЌвдCЮЊдВаФЃЌ1cmГЄЮЊАыОЖЛЁбCЃЌЕуPдкЁбCЩЯдЫЖЏЃЌСЌНгAPЃЌВЂНЋAPШЦЕуAЫГЪБеыа§зЊ60ЁужСAPЁфЃЌЕуDЪЧБпACЕФжаЕуЃЌСЌНгDPЁф.дкЕуPвЦЖЏЕФЙ§ГЬжаЃЌЯпЖЮDPЁфГЄЖШЕФзюаЁжЕЮЊ______cm.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕу![]() ЮЊ
ЮЊ![]() ЕФФкаФЃЌЙ§Еу
ЕФФкаФЃЌЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЕФГЄЮЊЃЈ ЃЉ
ЕФГЄЮЊЃЈ ЃЉ
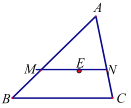
A.3ЃЎ5B.4C.5D.5ЃЎ5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌФГДѓТЅЕФЖЅВПЪїгавЛПщЙуИцХЦCDЃЌаЁРюдкЩНЦТЕФЦТНХAДІВтЕУЙуИцХЦЕзВПDЕФбіНЧЮЊ60ЁуЃЎбиЦТУцABЯђЩЯзпЕНBДІВтЕУЙуИцХЦЖЅВПCЕФбіНЧЮЊ45ЁуЃЌвбжЊЩНЦТABЕФЦТЖШi=1ЃК![]() ЃЌAB=10УзЃЌAE=15УзЃЎЃЈi=1ЃК
ЃЌAB=10УзЃЌAE=15УзЃЎЃЈi=1ЃК![]() ЪЧжИЦТУцЕФЧІжБИпЖШBHгыЫЎЦНПэЖШAHЕФБШЃЉ
ЪЧжИЦТУцЕФЧІжБИпЖШBHгыЫЎЦНПэЖШAHЕФБШЃЉ

ЃЈ1ЃЉЧѓЕуBОрЫЎЦНУцAEЕФИпЖШBHЃЛ
ЃЈ2ЃЉЧѓЙуИцХЦCDЕФИпЖШЃЎ
ЃЈВтНЧЦїЕФИпЖШКіТдВЛМЦЃЌНсЙћОЋШЗЕН0.1УзЃЎВЮПМЪ§ОнЃК![]() 1.414ЃЌ
1.414ЃЌ![]() 1.732ЃЉ
1.732ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬЕъзМБИЙКНјвЛХњЕчБљЯфКЭПеЕїЃЌУПЬЈЕчБљЯфЕФНјМлБШУПЬЈПеЕїЕФНјМлЖр400дЊЃЌЩЬЕъгУ8000дЊЙКНјЕчБљЯфЕФЪ§СПгыгУ6400дЊЙКНјПеЕїЕФЪ§СПЯрЕШЃЎ
ЃЈ1ЃЉЧѓУПЬЈЕчБљЯфгыПеЕїЕФНјМлЗжБ№ЪЧЖрЩйЃП
ЃЈ2ЃЉвбжЊЕчБљЯфЕФЯњЪлМлЮЊУПЬЈ2100дЊЃЌПеЕїЕФЯњЪлМлЮЊУПЬЈ1750дЊЃЎШєЩЬЕъзМБИЙКНјетСНжжМвЕчЙВ100ЬЈЃЌЦфжаЙКНјЕчБљЯфxЬЈЃЈ33ЁмxЁм40ЃЉЃЌФЧУДИУЩЬЕъвЊЛёЕУзюДѓРћШѓгІШчКЮНјЛѕЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com