
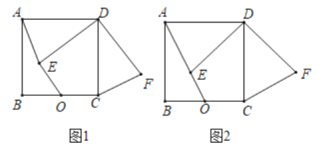
【题目】如图,正方形![]() 中,
中,![]() ,
,![]() 是
是![]() 边的中点,点
边的中点,点![]() 是正方形内一动点,
是正方形内一动点,![]() ,连接
,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得
得![]() ,连接
,连接![]() ,
,![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图2,若![]() ,
,![]() ,
,![]() 三点共线,求点
三点共线,求点![]() 到直线
到直线![]() 的距离.
的距离.
【答案】(1)证明见解析;(2)点F到直线BC的距离是![]() .
.
【解析】
(1)由旋转的性质可得∠EDF=90°,DE=DF,由正方形的性质可得∠ADC=90°,DE=DF,可得∠ADE=∠CDF,由“SAS”可证△ADE≌△CDF,可得AE=CF;
(2)由勾股定理可求AO的长,可得AE=CF=3,通过证明△ABO∽△CPF,可得![]() ,即可求PF的长,即可求点F到直线BC的距离.
,即可求PF的长,即可求点F到直线BC的距离.
解:(1)由旋转得:![]() ,
,![]() ,
,

∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
∵ ,
,
∴![]() ,
,
∴![]() ;
;
(2)解:如图2,过点F作FP⊥BC交BC延长线于点P,
则线段FP的长度就是点F到直线BC的距离.

∵点O是BC中点,且AB=BC=2![]()
∴BO=![]() ,
,
∴AO=![]() =5
=5
∵OE=2
∴AE=AO-OE=3
∵△ADE≌△CDF
∴AE=CF=3,∠DAO=∠DCF
∴∠BAO=∠FCP,且∠ABO=∠FPC=90°
∴△ABO∽△CPF
∴![]()
∴![]()
∴PF=![]()
∴点F到直线BC的距离为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠CAB=90°,AB=AC,点A在y轴上,BC∥x轴,点B![]() .将△ABC绕点A顺时针旋转的△AB′C′,当点B′落在x轴的正半轴上时,点C′的坐标为( )
.将△ABC绕点A顺时针旋转的△AB′C′,当点B′落在x轴的正半轴上时,点C′的坐标为( )
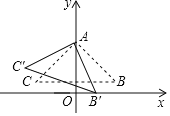
A.(﹣![]() ,
,![]() ﹣1)B.(﹣
﹣1)B.(﹣![]() ,
,![]() ﹣1)
﹣1)
C.(﹣![]() ,
,![]() +1)D.(﹣
+1)D.(﹣![]() ,
,![]() ﹣1)
﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们定义直线y=ax﹣a为抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
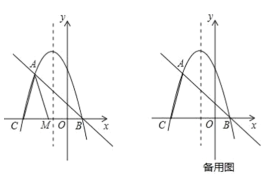
已知抛物线![]() 与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
(1)填空:该抛物线的“梦想直线”的解析式为 ,
(2)如图,点M为线段CB上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“梦想三角形”,求点N的坐标;
(3)当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形![]() 的边长为4,
的边长为4,![]() 是边
是边![]() 上的一个动点,连接
上的一个动点,连接![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,顶点
,顶点![]() 在线段
在线段![]() 上,对角线
上,对角线![]() ,
,![]() 相交于点
相交于点![]() .
.
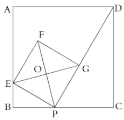

(1)若![]() ,则
,则![]() ;
;
(2)①求证:点![]() 一定在
一定在![]() 的外接圆上;
的外接圆上;
②当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,点
时,点![]() 也随之运动,求点
也随之运动,求点![]() 经过的路径长;
经过的路径长;
(3)在点![]() 从点
从点![]() 到点
到点![]() 的运动过程中,
的运动过程中,![]() 的外接圆的圆心也随之运动,求该圆心到边
的外接圆的圆心也随之运动,求该圆心到边![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租公司有若干辆同一型号的货车对外出租,每辆货车的日租金实行淡季、旺季两种价格标准,旺季每辆货车的日租金比淡季上涨![]() .据统计,淡季该公司平均每天有
.据统计,淡季该公司平均每天有![]() 辆货车未出租,日租金总收入为
辆货车未出租,日租金总收入为![]() 元;旺季所有的货车每天能全部租出,日租金总收入为
元;旺季所有的货车每天能全部租出,日租金总收入为![]() 元.
元.
(1)该出租公司这批对外出租的货车共有多少辆?淡季每辆货车的日租金多少元?
(2)经市场调查发现,在旺季如果每辆货车的日租金每上涨![]() 元,每天租出去的货车就会减少
元,每天租出去的货车就会减少![]() 辆,不考虑其它因素,每辆货车的日租金上涨多少元时,该出租公司的日租金总收入最高?
辆,不考虑其它因素,每辆货车的日租金上涨多少元时,该出租公司的日租金总收入最高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区在距离地面![]() 米的悬崖点
米的悬崖点![]() 处垂直水平线搭建了一个悬崖秋千,秋千拉绳均由钢管制作而成,当游客乘坐该秋千时,机器会将秋千拉至最高接近与地面平行的点
处垂直水平线搭建了一个悬崖秋千,秋千拉绳均由钢管制作而成,当游客乘坐该秋千时,机器会将秋千拉至最高接近与地面平行的点![]() 处(此时
处(此时![]() ) ,然后放下.该悬崖秋千以其惊险刺激立即成为网红打卡地.
) ,然后放下.该悬崖秋千以其惊险刺激立即成为网红打卡地.
![]() 若秋千放下
若秋千放下![]() 秒后
秒后![]() 点
点![]() 的垂直距离为
的垂直距离为![]() 米,求秋千拉绳
米,求秋千拉绳![]() 的长;
的长;
![]() 若某一时刻秋千荡至与点
若某一时刻秋千荡至与点![]() 水平距离相距
水平距离相距![]() 米的点
米的点![]() 处,求
处,求![]() 的度数,并求此时秋千底端距离悬崖底部多少米(结果保留整数参考数据:
的度数,并求此时秋千底端距离悬崖底部多少米(结果保留整数参考数据:![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
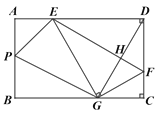
【题目】如图,在矩形ABCD中,点E,F分别在边AD,DC上,AB=6,DF=4,将矩形沿直线EF折叠,点D恰好落在BC边上的点G处,连接DG交EF于点H.
(1)求DE的长度.
(2)求![]() 的值.
的值.
(3)若AB边上有且只存在2个点P,使△APE与△BPG相似,请直接写出边AD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将函数y=![]() (x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com