
【题目】某出租公司有若干辆同一型号的货车对外出租,每辆货车的日租金实行淡季、旺季两种价格标准,旺季每辆货车的日租金比淡季上涨![]() .据统计,淡季该公司平均每天有
.据统计,淡季该公司平均每天有![]() 辆货车未出租,日租金总收入为
辆货车未出租,日租金总收入为![]() 元;旺季所有的货车每天能全部租出,日租金总收入为
元;旺季所有的货车每天能全部租出,日租金总收入为![]() 元.
元.
(1)该出租公司这批对外出租的货车共有多少辆?淡季每辆货车的日租金多少元?
(2)经市场调查发现,在旺季如果每辆货车的日租金每上涨![]() 元,每天租出去的货车就会减少
元,每天租出去的货车就会减少![]() 辆,不考虑其它因素,每辆货车的日租金上涨多少元时,该出租公司的日租金总收入最高?
辆,不考虑其它因素,每辆货车的日租金上涨多少元时,该出租公司的日租金总收入最高?
【答案】(1)该出租公司这批对外出租的货车共有![]() 辆,淡季每辆货车的日租金
辆,淡季每辆货车的日租金![]() 元;
元;
(2)每辆货车的日租金上涨![]() 元时,该出租公司的日租金总收入最高.
元时,该出租公司的日租金总收入最高.
【解析】
(1)该出租公司这批对外出租的货车共有![]() 辆,根据题意可以列出方程,进而求得结论;
辆,根据题意可以列出方程,进而求得结论;
(2)根据题意可以求得总收入和上涨价格之间的函数解析式,然后化为顶点式即可解答本题.
解:(1)该出租公司这批对外出租的货车共有![]() 辆,
辆,
根据题意得, ![]() ,
,
解得:![]() ,
,
经检验:![]() 是分式方程的根,
是分式方程的根,
![]() (元),
(元),
答:该出租公司这批对外出租的货车共有![]() 辆,淡季每辆货车的日租金
辆,淡季每辆货车的日租金![]() 元;
元;
(2)设每辆货车的日租金上涨![]() 元时,该出租公司的日租金总收入为
元时,该出租公司的日租金总收入为![]() 元,
元,
根据题意得,![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() 当
当![]() 时,
时,![]() 有最大值,
有最大值,
答:每辆货车的日租金上涨![]() 元时,该出租公司的日租金总收入最高.
元时,该出租公司的日租金总收入最高.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
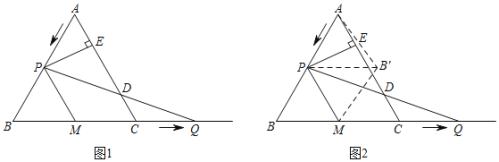
【题目】如图1,在等边△ABC中,AB=6cm,动点P从点A出发以1cm/s的速度沿AB匀速运动,动点Q同时从点C出发以同样的速度沿BC的延长线方向匀速运动,当点P到达点B时,点P、Q同时停止运动.设运动时间为t(s),过点P作PE⊥AC于E,PQ交AC边于D,线段BC的中点为M,连接PM.
(1)当t为何值时,△CDQ与△MPQ相似;
(2)在点P、Q运动过程中,点D、E也随之运动,线段DE的长度是否会发生变化?若发生变化,请说明理由,若不发生变化,求DE的长;
(3)如图2,将△BPM沿直线PM翻折,得△B'PM,连接AB',当t为何值时,AB'的值最小?并求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“每天锻炼一小时,健康生活一辈子”,学校准备从小明和小亮2人中随机选拔一人当“阳光大课间”领操员,体育老师设计的游戏规则是:将四张扑克牌(方块2、黑桃4、黑桃5、梅花5)的牌面如图1,扑克牌洗匀后,如图2背面朝上放置在桌面上.小亮和小明两人各抽取一张扑克牌,两张牌面数字之和为奇数时,小亮当选;否则小明当选.

(1)请用树状图或列表法求出所有可能的结果;
(2)请问这个游戏规则公平吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴,
轴,![]() 轴交于
轴交于![]() ,
,![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() ,
,![]() .
.

(1)求![]() 的值;
的值;
(2)求出直线![]() 的解析式;
的解析式;
(3)![]() 为线段
为线段![]() 上一点(不含端点),连接
上一点(不含端点),连接![]() ,一动点
,一动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 以每秒1个单位长度的速度运动到
以每秒1个单位长度的速度运动到![]() ,再沿线段
,再沿线段![]() 以每秒
以每秒![]() 个单位长度的速度运动到点
个单位长度的速度运动到点![]() 后停止,请直接写出点
后停止,请直接写出点![]() 在整个运动过程的最少用时.(提示:过点
在整个运动过程的最少用时.(提示:过点![]() 和点
和点![]() ,分别作
,分别作![]() 轴,
轴,![]() 轴的垂线
轴的垂线![]() ,
,![]() ,两垂线交于点
,两垂线交于点![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
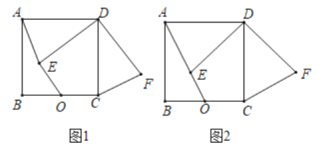
【题目】如图,正方形![]() 中,
中,![]() ,
,![]() 是
是![]() 边的中点,点
边的中点,点![]() 是正方形内一动点,
是正方形内一动点,![]() ,连接
,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得
得![]() ,连接
,连接![]() ,
,![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图2,若![]() ,
,![]() ,
,![]() 三点共线,求点
三点共线,求点![]() 到直线
到直线![]() 的距离.
的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 是以
是以![]() 为直径的半圆
为直径的半圆![]() 上任意一点(不与点
上任意一点(不与点![]() 重合),连接
重合),连接![]() 并延长至点
并延长至点![]() 使
使![]() 连接
连接![]() 交半圆
交半圆![]() 于点
于点![]() 过点
过点![]() 作
作![]() 于点
于点![]() .
.

![]() 求证:
求证:![]() .
.
![]() 如图2,连接
如图2,连接![]() .
.
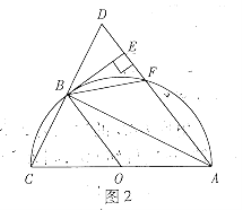
①当![]()
![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②当![]()
![]() 时,四边形
时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
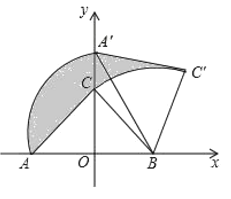
【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的点A'处,若AO=OB=2,则图中阴影部分面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,反比例函数y=![]() (x>0,k>0图象上的两点(n,3n)、(n+1,2n).
(x>0,k>0图象上的两点(n,3n)、(n+1,2n).
(1)求n的值;
(2)如图,直线l为正比例函数y=x的图象,点A在反比例函数y=![]() (x>0,k>0)的图象上,过点A作AB⊥l于点B,过点B作BC⊥x轴于点C,过点A作AD⊥BC于点D,记△BOC的面积为S1,△ABD的面积为S2,求S1﹣S2的值.
(x>0,k>0)的图象上,过点A作AB⊥l于点B,过点B作BC⊥x轴于点C,过点A作AD⊥BC于点D,记△BOC的面积为S1,△ABD的面积为S2,求S1﹣S2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
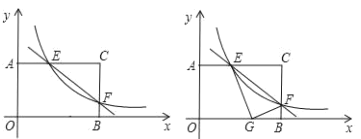
【题目】矩形AOBC中,OB=4,OA=3.分别以OB、OA所在直线为x轴、y轴,建立如图1所示的平面直角坐标系.F是BC边上一个动点(不与B、C重合).过点F的反比例函数y=![]() (k>0)的图象与边AC交于点E.
(k>0)的图象与边AC交于点E.
(1)当点F运动到边BC的中点时,点E的坐标为__________;
(2)连接EF,求∠EFC的正切值;
(3)如图2,将△CEF沿EF折叠,点C恰好落在边OB上的点G处,求BG的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com