
【题目】“每天锻炼一小时,健康生活一辈子”,学校准备从小明和小亮2人中随机选拔一人当“阳光大课间”领操员,体育老师设计的游戏规则是:将四张扑克牌(方块2、黑桃4、黑桃5、梅花5)的牌面如图1,扑克牌洗匀后,如图2背面朝上放置在桌面上.小亮和小明两人各抽取一张扑克牌,两张牌面数字之和为奇数时,小亮当选;否则小明当选.

(1)请用树状图或列表法求出所有可能的结果;
(2)请问这个游戏规则公平吗?并说明理由.
科目:初中数学 来源: 题型:
【题目】《孙子算经)是我国传统数学的重要著作之一,其中记载的“荡杯问题”非常有趣.原题是今有妇人河上荡杯,津吏问日:“杯何以多?”妇人日:“有客.”津吏日:“客几何?”妇人日:“两人共饭,三人共羹,四人共肉,凡用杯六十五.不知客几何?”
大意:一个妇女在河边洗碗,河官问:“洗多少碗?有多少客?”妇女答:“洗![]() 只碗,客人二人.共用一只饭碗,三人共用一只汤碗,四人共用一只肉碗.问:有多少客人用餐?”请解答上述问题.
只碗,客人二人.共用一只饭碗,三人共用一只汤碗,四人共用一只肉碗.问:有多少客人用餐?”请解答上述问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的边长为5,E在BC边上运动,DE的中点G,EG绕E顺时针旋转90°得EF,问CE为多少时A、C、F在一条直线上( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校团委为了教育学生,开展了以感恩为主题的有奖征文活动,并为获奖的同学颁发奖品.小红与小明去文化商店购买甲、乙两种笔记本作为奖品,若买甲种笔记本20个,乙种笔记本10个,共用110元;且买甲种笔记本30个比买乙种笔记本20个少花10元.
(1)求甲、乙两种笔记本的单价各是多少元?
(2)若本次购进甲种笔记本的数量比乙种笔记本的数量的2倍还少10个,且购进两种笔记本的总数量不少于80本,总金额不超过320元.请你设计出本次购进甲、乙两种笔记本的所有方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
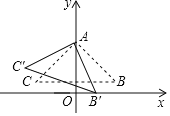
【题目】如图,在Rt△ABC中,∠CAB=90°,AB=AC,点A在y轴上,BC∥x轴,点B![]() .将△ABC绕点A顺时针旋转的△AB′C′,当点B′落在x轴的正半轴上时,点C′的坐标为( )
.将△ABC绕点A顺时针旋转的△AB′C′,当点B′落在x轴的正半轴上时,点C′的坐标为( )
A.(﹣![]() ,
,![]() ﹣1)B.(﹣
﹣1)B.(﹣![]() ,
,![]() ﹣1)
﹣1)
C.(﹣![]() ,
,![]() +1)D.(﹣
+1)D.(﹣![]() ,
,![]() ﹣1)
﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(0,4),B(7,0),C(7,4),连接AC,BC得到矩形AOBC,点D的边AC上,将边OA沿OD折叠,点A的对应边为A'.若点A'到矩形较长两对边的距离之比为1:3,则点A'的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们定义直线y=ax﹣a为抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
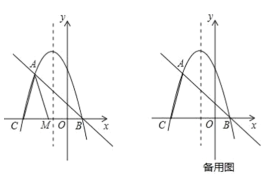
已知抛物线![]() 与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
(1)填空:该抛物线的“梦想直线”的解析式为 ,
(2)如图,点M为线段CB上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“梦想三角形”,求点N的坐标;
(3)当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租公司有若干辆同一型号的货车对外出租,每辆货车的日租金实行淡季、旺季两种价格标准,旺季每辆货车的日租金比淡季上涨![]() .据统计,淡季该公司平均每天有
.据统计,淡季该公司平均每天有![]() 辆货车未出租,日租金总收入为
辆货车未出租,日租金总收入为![]() 元;旺季所有的货车每天能全部租出,日租金总收入为
元;旺季所有的货车每天能全部租出,日租金总收入为![]() 元.
元.
(1)该出租公司这批对外出租的货车共有多少辆?淡季每辆货车的日租金多少元?
(2)经市场调查发现,在旺季如果每辆货车的日租金每上涨![]() 元,每天租出去的货车就会减少
元,每天租出去的货车就会减少![]() 辆,不考虑其它因素,每辆货车的日租金上涨多少元时,该出租公司的日租金总收入最高?
辆,不考虑其它因素,每辆货车的日租金上涨多少元时,该出租公司的日租金总收入最高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正确结论的序号是 .
.其中正确结论的序号是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com