
【题目】已知正方形ABCD的边长为5,E在BC边上运动,DE的中点G,EG绕E顺时针旋转90°得EF,问CE为多少时A、C、F在一条直线上( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰三角形,AB=AC,点D是AB上一点,过点D作DE⊥BC交BC于点E,交CA延长线于点F.
(1)证明:△ADF是等腰三角形;
(2)若∠B=60°,BD=4,AD=2,求EC的长,

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABD和△BCD都是等边三角形,E、F分别是边AD、CD上的点,且DE=CF,连接BE、EF、FB.
求证:(1)△ABE≌△DBF;
(2)△BEF是等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有![]() 、
、![]() 、
、![]() 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )

A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边垂直平分线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边中线的交点处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC, 点M在△ABC内,点P在线段MC上,∠ABP=2∠ACM.

(1)若∠PBC=10°,∠BAC=80°,求∠MPB的值
(2)若点M在底边BC的中线上,且BP=AC,试探究∠A与∠ABP之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AB=AC,D是BC的中点,动点E在边AB上(点E不与点A,B重合), 动点F在射线AC上,连结DE, DF.
(1)如图1,当∠DEB=∠DFC=90°时,直接写出DE与DF的数量关系;

(2)如图2,当∠DEB+∠DFC=180°(∠DEB≠∠DFC)时,猜想DE与DF的数量关系,并证明;

(3)当点E,D,F在同一条直线上时,
①依题意补全图3;
②在点E运动的过程中,是否存在EB=FC? ( 填“存在”或“不存在” ).

查看答案和解析>>
科目:初中数学 来源: 题型:
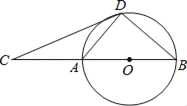
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)若BC=6,tan∠CDA=![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学有库存1800套旧桌凳,修理后捐助贫困山区学校.现有甲,乙两个木工组都想承揽这项业务.经协商后得知:甲木工组每天修理的桌凳套数是乙木工组每天修理桌凳套数的![]() ,甲木工组单独修理这批桌凳的天数比乙木工组单独修理这批桌凳的天数多10天,甲木工组每天的修理费用是600元,乙木工组每天的修理费用是800元.
,甲木工组单独修理这批桌凳的天数比乙木工组单独修理这批桌凳的天数多10天,甲木工组每天的修理费用是600元,乙木工组每天的修理费用是800元.
(1)求甲,乙两木工组单独修理这批桌凳的天数;
(2)现有三种修理方案供选择:方案一,由甲木工组单独修理这批桌凳;方案二,由乙木工组单独修理这批桌凳;方案三,由甲,乙两个木工组共同合作修理这批桌凳.请计算说明哪种方案学校付的修理费最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AA1,A1A2,A2A3,A3B,AB分别是五个半圆的直径,两只小虫同时出发,以相同的速度从点A到点B,甲虫沿ADA1,A1EA2,A2FA3,A3GB路线爬行,乙虫沿ACB路线爬行,则下列结论正确的是( )

A. 甲先到点B B. 乙先到点B C. 甲、乙同时到点B D. 无法确定谁先到点B
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com