
【题目】如图所示,△ABD和△BCD都是等边三角形,E、F分别是边AD、CD上的点,且DE=CF,连接BE、EF、FB.
求证:(1)△ABE≌△DBF;
(2)△BEF是等边三角形.

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】综合与实践﹣猜想、证明与拓广
问题情境:
数学课上同学们探究正方形边上的动点引发的有关问题,如图1,正方形ABCD中,点E是BC边上的一点,点D关于直线AE的对称点为点F,直线DF交AB于点H,直线FB与直线AE交于点G,连接DG,CG.
猜想证明
(1)当图1中的点E与点B重合时得到图2,此时点G也与点B重合,点H与点A重合.同学们发现线段GF与GD有确定的数量关系和位置关系,其结论为: ;
(2)希望小组的同学发现,图1中的点E在边BC上运动时,(1)中结论始终成立,为证明这两个结论,同学们展开了讨论:
小敏:根据轴对称的性质,很容易得到“GF与GD的数量关系”…
小丽:连接AF,图中出现新的等腰三角形,如△AFB,…
小凯:不妨设图中不断变化的角∠BAF的度数为n,并设法用n表示图中的一些角,可证明结论.
请你参考同学们的思路,完成证明;
(3)创新小组的同学在图1中,发现线段CG∥DF,请你说明理由;
联系拓广:
(4)如图3若将题中的“正方形ABCD”变为“菱形ABCD“,∠ABC=α,其余条件不变,请探究∠DFG的度数,并直接写出结果(用含α的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长度为1个单位长度的小正方形组成的正方形中,点A,B,C在小正方形的顶点上.

(1)在图中画出与△ABC关于直线l成轴对称的△A′B′C′
(2)三角形ABC的面积为 ;
(3)在直线l上找一点P,使PA+PB的长最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰Rt△ACB,∠ACB=90°,AC=BC,点A、C分别在x轴、y轴的正半轴上.

(1)如图1,求证:∠BCO=∠CAO
(2)如图2,若OA=5,OC=2,求B点的坐标
(3)如图3,点C(0,3),Q、A两点均在x轴上,且S△CQA=18.分别以AC、CQ为腰在第一、第二象限作等腰Rt△CAN、等腰Rt△QCM,连接MN交y轴于P点,OP的长度是否发生改变?若不变,求出OP的值;若变化,求OP的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一数值转换器,原理如图所示,如果开始输入![]() 的值为1,则第一次输出的结果是4,第二次输出的结果是5,……;那么2021次输出的结果是 _________ .
的值为1,则第一次输出的结果是4,第二次输出的结果是5,……;那么2021次输出的结果是 _________ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=( )
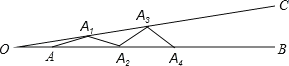
A. 10B. 9C. 8D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的边长为5,E在BC边上运动,DE的中点G,EG绕E顺时针旋转90°得EF,问CE为多少时A、C、F在一条直线上( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)
由于雾霾天气频发,市场上防护口罩出现热销.某药店准备购进一批口罩,已知1个A型口罩和3个B型口罩共需26元;3个A型口罩和2个B型口罩共需29元.
⑴ 求一个A型口罩和一个B型口罩的售价各是多少元?
⑵ 药店准备购进这两种型号的口罩共50个,其中A型口罩数量不少于35个,且不多于B型口罩的3倍,有哪几种购买方案,哪种方案最省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com