
【题目】已知点A(0,4),B(7,0),C(7,4),连接AC,BC得到矩形AOBC,点D的边AC上,将边OA沿OD折叠,点A的对应边为A'.若点A'到矩形较长两对边的距离之比为1:3,则点A'的坐标为 .
【答案】
【解析】
解:由点A(0,4),B(7,0),C(7,4),可得BC=OA=4,OB=AC=7,
分两种情况:
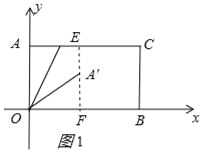
(1)当点A'在矩形AOBC的内部时,过A'作OB的垂线交OB于F,交AC于E,如图1所示:
①当A'E:A'F=1:3时,
∵A'E+A'F=BC=4,
∴A'E=1,A'F=3,
由折叠的性质得:OA'=OA=4,
在Rt△OA'F中,由勾股定理得:OF=![]() ,
,
∴A'(![]() ,3);
,3);
②当A'E:A'F=3:1时,同理得:A'(![]() ,1);
,1);
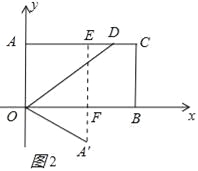
(2)当点A'在矩形AOBC的外部时,此时点A'在第四象限,过A'作OB的垂线交OB于F,交AC于E,如图2所示:∵A'F:A'E=1:3,则A'F:EF=1:2,
∴A'F=![]() EF=
EF=![]() BC=2,
BC=2,
由折叠的性质得:OA'=OA=4,
在Rt△OA'F中,由勾股定理得:OF=![]() =2
=2![]() ,
,
∴A'(2![]() ,﹣2);
,﹣2);
故答案为(![]() ,3)或(
,3)或(![]() ,1)或(2
,1)或(2![]() ,﹣2).
,﹣2).


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,∠ADC的平分线与AB交于E,点F在DE的延长线上,∠BFE=90°,连接AF、CF,CF与AB交于G.有以下结论:
①AE=BC
②AF=CF
③BF2=FGFC
④EGAE=BGAB
其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.

(1)求证:AE与⊙O相切;
(2)当BC=4,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,且
上,且![]() ,以
,以![]() 为圆心,
为圆心,![]() 长为半径作圆,
长为半径作圆,![]() 经过点
经过点![]() ,与
,与![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() .
.

(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的半径;
的半径;
(3)在(2)的条件下,若![]() 的内切圆圆心为
的内切圆圆心为![]() ,直接写出
,直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“每天锻炼一小时,健康生活一辈子”,学校准备从小明和小亮2人中随机选拔一人当“阳光大课间”领操员,体育老师设计的游戏规则是:将四张扑克牌(方块2、黑桃4、黑桃5、梅花5)的牌面如图1,扑克牌洗匀后,如图2背面朝上放置在桌面上.小亮和小明两人各抽取一张扑克牌,两张牌面数字之和为奇数时,小亮当选;否则小明当选.

(1)请用树状图或列表法求出所有可能的结果;
(2)请问这个游戏规则公平吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
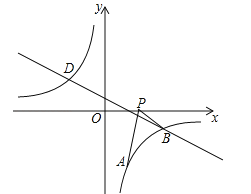
【题目】(2016湖北省黄冈市)如图,已知点A(1,a)是反比例函数![]() 的图象上一点,直线
的图象上一点,直线![]() 与反比例函数
与反比例函数![]() 的图象在第四象限的交点为点B.
的图象在第四象限的交点为点B.
(1)求直线AB的解析式;
(2)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.
【答案】(1)y=x﹣4;(2)P(4,0).
【解析】试题分析:(1)先把A(1,a)代入反比例函数解析式求出a得到A点坐标,再解方程组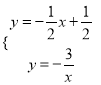 ,得B点坐标,然后利用待定系数法求AB的解析式;
,得B点坐标,然后利用待定系数法求AB的解析式;
(2)直线AB交x轴于点Q,如图,利用x轴上点的坐标特征得到Q点坐标,则PA﹣PB≤AB(当P、A、B共线时取等号),于是可判断当P点运动到Q点时,线段PA与线段PB之差达到最大,从而得到P点坐标.
试题解析:(1)把A(1,a)代入![]() 得a=﹣3,则A(1,﹣3),解方程组:
得a=﹣3,则A(1,﹣3),解方程组: 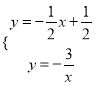 ,得:
,得: ![]() 或
或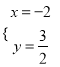 ,则B(3,﹣1),设直线AB的解析式为y=kx+b,把A(1,﹣3),B(3,﹣1)代入得:
,则B(3,﹣1),设直线AB的解析式为y=kx+b,把A(1,﹣3),B(3,﹣1)代入得: ![]() ,解得:
,解得: ![]() ,所以直线AB的解析式为y=x﹣4;
,所以直线AB的解析式为y=x﹣4;
(2)直线AB交x轴于点Q,如图,当y=0时,x﹣4=0,解得x=4,则Q(4,0),因为PA﹣PB≤AB(当P、A、B共线时取等号),所以当P点运动到Q点时,线段PA与线段PB之差达到最大,此时P点坐标为(4,0).
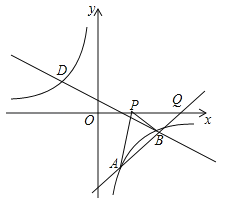
考点:反比例函数与一次函数的交点问题.
【题型】解答题
【结束】
22
【题目】成都三圣乡花卉基地出售两种盆栽花卉:太阳花6元/盆,绣球花10元/盆.若一次购买的绣球花超过20盆时,超过20盆部分的绣球花价格打8折.
(1)若小张家花台绿化需用60盆两种盆栽花卉,小张爸爸给他460元钱去购买,问两种花卉各买了多少盆?
(2)分别写出两种花卉的付款金额y(元)关于购买量x(盆)的函数解析式;
(3)为了美化环境,花园小区计划到该基地购买这两种花卉共90盆,其中太阳花数量不超过绣球花数量的一半.两种花卉各买多少盆时,总费用最少,最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴,
轴,![]() 轴交于
轴交于![]() ,
,![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() ,
,![]() .
.

(1)求![]() 的值;
的值;
(2)求出直线![]() 的解析式;
的解析式;
(3)![]() 为线段
为线段![]() 上一点(不含端点),连接
上一点(不含端点),连接![]() ,一动点
,一动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 以每秒1个单位长度的速度运动到
以每秒1个单位长度的速度运动到![]() ,再沿线段
,再沿线段![]() 以每秒
以每秒![]() 个单位长度的速度运动到点
个单位长度的速度运动到点![]() 后停止,请直接写出点
后停止,请直接写出点![]() 在整个运动过程的最少用时.(提示:过点
在整个运动过程的最少用时.(提示:过点![]() 和点
和点![]() ,分别作
,分别作![]() 轴,
轴,![]() 轴的垂线
轴的垂线![]() ,
,![]() ,两垂线交于点
,两垂线交于点![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 是以
是以![]() 为直径的半圆
为直径的半圆![]() 上任意一点(不与点
上任意一点(不与点![]() 重合),连接
重合),连接![]() 并延长至点
并延长至点![]() 使
使![]() 连接
连接![]() 交半圆
交半圆![]() 于点
于点![]() 过点
过点![]() 作
作![]() 于点
于点![]() .
.

![]() 求证:
求证:![]() .
.
![]() 如图2,连接
如图2,连接![]() .
.
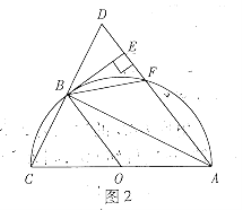
①当![]()
![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②当![]()
![]() 时,四边形
时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过点A(0,-6)的抛物线y=![]() x2+bx+c与x轴相交于B(-2,0),C两点.
x2+bx+c与x轴相交于B(-2,0),C两点.
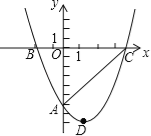
(1)求此抛物线的函数关系式和顶点D的坐标;
(2)将(1)中求得的抛物线向左平移1个单位长度,再向上平移m(m>0)个单位长度得到新抛物线y1,若新抛物线y1的顶点P在△ABC内,求m的取值范围;
(3)设点M在y轴上,∠OMB+∠OAB=∠ACB,直接写出AM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com