
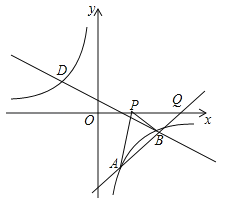
����Ŀ����2016����ʡ�Ƹ��У���ͼ����֪��A��1��a���Ƿ���������![]() ��ͼ����һ�㣬ֱ��
��ͼ����һ�㣬ֱ��![]() �뷴��������
�뷴��������![]() ��ͼ���ڵ������Ľ���Ϊ��B��
��ͼ���ڵ������Ľ���Ϊ��B��
��1����ֱ��AB�Ľ���ʽ��
��2������P��x��0����x������������˶������߶�PA���߶�PB֮��ﵽ���ʱ�����P�����꣮
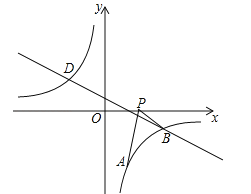
���𰸡���1��y=x��4����2��P��4��0����
�������������������1���Ȱ�A��1��a�����뷴������������ʽ���a�õ�A�����꣬�ٽⷽ����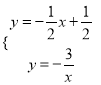 ����B�����꣬Ȼ�����ô���ϵ������AB�Ľ���ʽ��
����B�����꣬Ȼ�����ô���ϵ������AB�Ľ���ʽ��
��2��ֱ��AB��x���ڵ�Q����ͼ������x���ϵ�����������õ�Q�����꣬��PA��PB��AB����P��A��B����ʱȡ�Ⱥţ������ǿ��жϵ�P���˶���Q��ʱ���߶�PA���߶�PB֮��ﵽ��Ӷ��õ�P�����꣮
�����������1����A��1��a������![]() ��a=��3����A��1����3�����ⷽ���飺
��a=��3����A��1����3�����ⷽ���飺 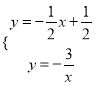 ���ã�
���ã� ![]() ��
��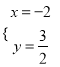 ����B��3����1������ֱ��AB�Ľ���ʽΪy=kx+b����A��1����3����B��3����1������ã�
����B��3����1������ֱ��AB�Ľ���ʽΪy=kx+b����A��1����3����B��3����1������ã� ![]() ����ã�
����ã� ![]() ������ֱ��AB�Ľ���ʽΪy=x��4��
������ֱ��AB�Ľ���ʽΪy=x��4��
��2��ֱ��AB��x���ڵ�Q����ͼ����y=0ʱ��x��4=0�����x=4����Q��4��0������ΪPA��PB��AB����P��A��B����ʱȡ�Ⱥţ������Ե�P���˶���Q��ʱ���߶�PA���߶�PB֮��ﵽ���ʱP������Ϊ��4��0����
���㣺������������һ�κ����Ľ������⣮
�����͡������
��������
22
����Ŀ���ɶ���ʥ�绨�ܻ��س����������Ի��ܣ�̫����6Ԫ/�裬����10Ԫ/�裮��һ�ι����������20��ʱ������20�貿�ֵ����۸��8�ۣ�
��1����С�żһ�̨�̻�����60���������Ի��ܣ�С�Űְָ���460ԪǮȥ���������ֻ��ܸ����˶����裿
��2���ֱ�д�����ֻ��ܵĸ�����y��Ԫ�����ڹ�����x���裩�ĺ�������ʽ��
��3��Ϊ��������������С���ƻ����û��ع��������ֻ��ܹ�90�裬����̫������������������������һ�룮���ֻ��ܸ��������ʱ���ܷ������٣����ٷ����Ƕ���Ԫ��
���𰸡���1������̫����35�裬����25������2�����ĸ�����y��Ԫ�����ڹ�����x���裩�ĺ�������ʽ�ǣ�y=![]() ����3��̫����30�裬����60��ʱ���ܷ������٣����ٷ�����700Ԫ��
����3��̫����30�裬����60��ʱ���ܷ������٣����ٷ�����700Ԫ��
�������������������1�����������г���������⼴�ɣ�
��2�����ȸ����ܼ�=���ۡ����������̫�����ĸ�����y��Ԫ�����ڹ�����x���裩�ĺ�������ʽ��Ȼ��������������һ�ι������������20�裻��һ�ι����������20�裻�����ܼ�=���ۡ�������������ĸ�����y��Ԫ�����ڹ�����x���裩�ĺ�������ʽ���ɣ�
��3������̫������������������������һ�룬�ɵ�̫�����������������ֻ�������![]() ����̫��������������30�裬������������������60�裻Ȼ����̫������������x�裬������������90-x�裬�����ܼ�=���ۡ�����������������ֻ����ܷ����Ƕ��٣������жϳ����ֻ��ܸ��������ʱ���ܷ������٣����ٷ����Ƕ���Ԫ���ɣ�
����̫��������������30�裬������������������60�裻Ȼ����̫������������x�裬������������90-x�裬�����ܼ�=���ۡ�����������������ֻ����ܷ����Ƕ��٣������жϳ����ֻ��ܸ��������ʱ���ܷ������٣����ٷ����Ƕ���Ԫ���ɣ�
�����������1���蹺��̫����x�裬����y��,��������ã�
![]()
��ã�![]()
�ʹ���̫����35�裬����25��.
��2��̫�����ĸ�����y��Ԫ�����ڹ�����x���裩�ĺ�������ʽ�ǣ�y=6x��
��һ�ι������������20��ʱ��
������y��Ԫ�����ڹ�����x���裩�ĺ�������ʽ�ǣ�y=10x��x��20����
��һ�ι����������20��ʱ��
������y��Ԫ�����ڹ�����x���裩�ĺ�������ʽ�ǣ�
y=10��20+10��0.8����x-20��
=200+8x-160
=8x+40
���ϣ��ɵ�
���ĸ�����y��Ԫ�����ڹ�����x���裩�ĺ�������ʽ�ǣ�
y=![]()
��3���������⣬�ɵ�̫����������������90��![]() ��30(��)��
��30(��)��
�����������������ڣ�90-30=60���裩��
��̫������������x�裬������������90-x�裬�������ֻ����ܷ�����yԪ��
��x��30��
��y=6x+[8��90-x��+40]
=6x+[760-8x]
=760-2x
��Ϊx��30��
���Ե�x=30ʱ��
ymin=760-2��30=700��Ԫ����
��̫����30�裬����60��ʱ���ܷ������٣����ٷ�����700Ԫ��
��̫����30�裬����60��ʱ���ܷ������٣����ٷ�����700Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ھ���ֽƬABCD�У�AB=3cm��AD=5cm���۵�ֽƬʹB�����ڱ�AD�ϵ�E�����ۺ�ΪPQ������E��EF��AB��PQ��F������BF��
��1����֤���ı���BFEPΪ���Σ�
��2������E��AD�����ƶ�ʱ���ۺ۵Ķ˵�P��QҲ��֮�ƶ���
�ٵ���Q���C�غ�ʱ����ͼ2����������BFEP�ı߳���
������P��Q�ֱ��ڱ�BA��BC���ƶ��������E�ڱ�AD���ƶ��������룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)���ⷢ��
��ͼ1,��ACB����DCE��Ϊ����ֱ��������,��ACB=90��,B,C,D��һ��ֱ����.
���:�߶�AD,BE֮��Ĺ�ϵΪ .
(2)��չ̽��
��ͼ2,��ACB����DCE��Ϊ����ֱ��������,��ACB=��DCE=90��,���ж�AD,BE�Ĺ�ϵ,��˵������.
(3)�������
��ͼ3,�߶�PA=3,��B���߶�PA��һ��,PB=5,����AB,��AB�Ƶ�A��ʱ����ת90��õ��߶�AC,���ŵ�B��λ�õı仯,ֱ��д��PC�ķ�Χ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABD�У�AC��BD��C����EΪAC��һ�㣬����BE��DE��DE���ӳ��߽�AB��F����֪DE=AB����CAD=45����
��1����֤��DF��AB��
��2������ͼ����Ӱ���������ɹ��ɶ�����֤������֪����ͼ���ڡ�ABC�У���ACB=90����BC=a��AC=b��AB=c����֤��a2+b2=c2��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1���߶�AC��6cm���߶�BC��15cm����M��AC���е㣬��CB��ȡһ��N��ʹ��CN��NB��1��2����MN�ij���

��2����ͼ2����CΪ�߶�AB������һ�㣬����AC+CB��acm��M��N�ֱ�ΪAC��BC���е㣬���ܲ���MN�ij����𣿲�˵�����ɣ�
��3����C���߶�AB���ӳ����ϵ�һ�㣬������AC��BC��bcm��M��N�ֱ�ΪAC��BC���е㣬���ܲ���MN�ij����𣿲�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
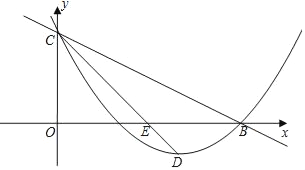
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y=ax2��2x+c��ֱ��y=��![]() x+3�ֱ���x�ᡢy���ϵ�B��C���㣬�����ߵĶ���Ϊ��D������CD��x���ڵ�E��
x+3�ֱ���x�ᡢy���ϵ�B��C���㣬�����ߵĶ���Ϊ��D������CD��x���ڵ�E��
��1���������ߵĽ���ʽ�Լ���D�����ꣻ
��2����tan��BCD��
��3����P��ֱ��BC�ϣ�����PEB=��BCD�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ 1����һ�ž���ֽƬ ABCD ���ŶԽ��� BD �����۵������� C �䵽�� E ����BE��AD �ڵ� F.
��1����֤����BDF �ǵ��������Σ�
��2����ͼ 2������ D �� DG��BE���� BC �ڵ� G������ FG �� BD �ڵ� O��
���ж��ı��� BFDG ����״����˵�����ɣ�

���� AD=AB+2��BD=10�����ı��� BFDG �������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������״��С��ȫ��ͬ��С�����ο�Ƭ(��ͼ1)���ص��ط���һ������Ϊ������(��Ϊmcm����Ϊncm)�ĺ��ӵĵײ�(��ͼ2)�����ӵ���δ����Ƭ���ǵIJ�������Ӱ��ʾ.��ͼ2��������Ӱ���ֵ��ܳ����ǣ� ��

A. 4mcmB. 4ncmC. 2(m+n)cmD. 4(mn)cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳���16����E�ڱ�AB�ϣ�AE=3����F�DZ�BC�ϲ����B��C�غϵ�һ�����㣬����EBF��EF�۵�����B����B�䴦������CDB��ǡΪ���������Σ���DB��ij�Ϊ_____��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com