
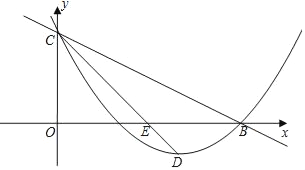
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2﹣2x+c与直线y=﹣![]() x+3分别交于x轴、y轴上的B、C两点,抛物线的顶点为点D,联结CD交x轴于点E.
x+3分别交于x轴、y轴上的B、C两点,抛物线的顶点为点D,联结CD交x轴于点E.
(1)求抛物线的解析式以及点D的坐标;
(2)求tan∠BCD;
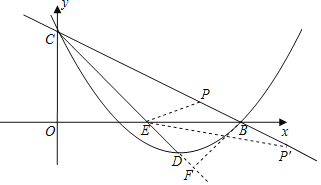
(3)点P在直线BC上,若∠PEB=∠BCD,求点P的坐标.
【答案】(1)D(4,﹣1);(2)![]() ;(3)点P(
;(3)点P(![]() ,
,![]() )或(12,﹣3).
)或(12,﹣3).
【解析】分析:(1)直接利用待定系数法求出二次函数解析式进而得出答案;
(2)利用锐角三角函数关系得出EC,BF的长,进而得出答案;
(3)分别利用①点P在x轴上方,②点P在x轴下方,分别得出点P的坐标.
详解:(1)由题意得B(6,0),C(0,3),
把B(6,0)C(0,3)代入y=ax2-2x+c
得![]() ,
,
解得:![]() ,
,
∴抛物线的解析式为:y=![]() x2-2x+3
x2-2x+3
=![]() (x2-8x)+3
(x2-8x)+3
=![]() (x-4)2-1,
(x-4)2-1,
∴D(4,-1);
(2)可得点E(3,0),
OE=OC=3,∠OEC=45°,
过点B作BF⊥CD,垂足为点F
在Rt△OEC中,EC=![]() ,
,
在Rt△BEF中,BF=BEsin∠BEF=![]() ,
,
同理,EF=![]() ,
,
∴CF=![]() +
+![]() =
=![]() ,
,
在Rt△CBF中,tan∠BCD=![]() ;
;
(3)设点P(m,![]() m+3)
m+3)
∵∠PEB=∠BCD,
∴tan∠PEB=tan∠BCD=![]() ,
,
①点P在x轴上方
∴![]() ,
,
解得:m=![]() ,
,
∴点P(![]() ,
,![]() ),
),
②点P在x轴下方
∴![]() ,
,
解得:m=12,
∴点P(12,-3),
综上所述,点P(![]() ,
,![]() )或(12,-3).
)或(12,-3).


科目:初中数学 来源: 题型:
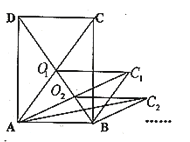
【题目】如图所示,矩形![]() 的面积为
的面积为![]() ,它的两条对角线交于点
,它的两条对角线交于点![]() ,以
,以![]() 、
、![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,平行四边形
,平行四边形![]() 的对角线交于点
的对角线交于点![]() ,同样以
,同样以![]() 、
、![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,……,依次类推,则平行四边形
,……,依次类推,则平行四边形![]() 的面积为( )
的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李师傅在某加工厂工作,厂里规定每个工人平均每天生产零件40个,一周7天生产280个,但由于种种原因,实际每天生产个数与计划相比有出入.下表是李师傅某周的生产情况(超产记为正、减产记为负):

(1)根据记录的数据可知李师傅星期四生产零件______个.
(2)根据记录的数据可知李师傅本周实际生产零件______个.
(3)该厂实行“每周计件工资制”.每生产一个零件可得工资10元,若超额完成任务,则超过部分每个另奖5元;少生产一个则倒扣3元,那么李师傅这一周的工资总额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
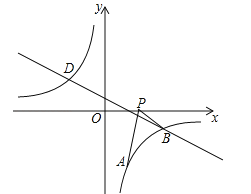
【题目】(2016湖北省黄冈市)如图,已知点A(1,a)是反比例函数![]() 的图象上一点,直线
的图象上一点,直线![]() 与反比例函数
与反比例函数![]() 的图象在第四象限的交点为点B.
的图象在第四象限的交点为点B.
(1)求直线AB的解析式;
(2)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.
【答案】(1)y=x﹣4;(2)P(4,0).
【解析】试题分析:(1)先把A(1,a)代入反比例函数解析式求出a得到A点坐标,再解方程组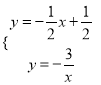 ,得B点坐标,然后利用待定系数法求AB的解析式;
,得B点坐标,然后利用待定系数法求AB的解析式;
(2)直线AB交x轴于点Q,如图,利用x轴上点的坐标特征得到Q点坐标,则PA﹣PB≤AB(当P、A、B共线时取等号),于是可判断当P点运动到Q点时,线段PA与线段PB之差达到最大,从而得到P点坐标.
试题解析:(1)把A(1,a)代入![]() 得a=﹣3,则A(1,﹣3),解方程组:
得a=﹣3,则A(1,﹣3),解方程组: 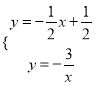 ,得:
,得: ![]() 或
或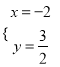 ,则B(3,﹣1),设直线AB的解析式为y=kx+b,把A(1,﹣3),B(3,﹣1)代入得:
,则B(3,﹣1),设直线AB的解析式为y=kx+b,把A(1,﹣3),B(3,﹣1)代入得: ![]() ,解得:
,解得: ![]() ,所以直线AB的解析式为y=x﹣4;
,所以直线AB的解析式为y=x﹣4;
(2)直线AB交x轴于点Q,如图,当y=0时,x﹣4=0,解得x=4,则Q(4,0),因为PA﹣PB≤AB(当P、A、B共线时取等号),所以当P点运动到Q点时,线段PA与线段PB之差达到最大,此时P点坐标为(4,0).
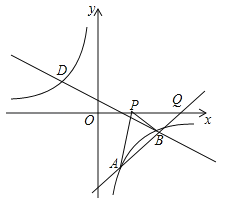
考点:反比例函数与一次函数的交点问题.
【题型】解答题
【结束】
22
【题目】成都三圣乡花卉基地出售两种盆栽花卉:太阳花6元/盆,绣球花10元/盆.若一次购买的绣球花超过20盆时,超过20盆部分的绣球花价格打8折.
(1)若小张家花台绿化需用60盆两种盆栽花卉,小张爸爸给他460元钱去购买,问两种花卉各买了多少盆?
(2)分别写出两种花卉的付款金额y(元)关于购买量x(盆)的函数解析式;
(3)为了美化环境,花园小区计划到该基地购买这两种花卉共90盆,其中太阳花数量不超过绣球花数量的一半.两种花卉各买多少盆时,总费用最少,最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省某旅游景点的旅客人数逐年增加,据旅游部门统计,2016年约为120万人次,预计2018年约为170万人次,设游客人数年平均增长率为x,则下列方程中正确的是( )
A. 120(1+x)=170 B. 170(1﹣x)=120
C. 120(1+x)2=170 D. 120+120(1+x)+120(1+x)2=170
查看答案和解析>>
科目:初中数学 来源: 题型:
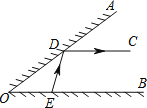
【题目】如图,△AOB的边OA半面镜.∠AOB=36°,在OB边上有点E,从点E射出一束光线经平面镜反射后,反射光线DC恰好满足DC∥OB,已知入射光线、反射光线与半面镜的夹角相等,即∠ODE=∠ADC,求∠DEB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
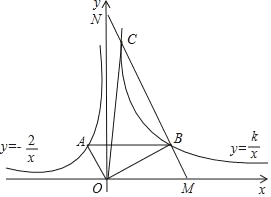
【题目】如图,∠AOB=90°,反比例函数y=﹣![]() (x<0)的图象过点A(﹣1,a),反比例函数y=
(x<0)的图象过点A(﹣1,a),反比例函数y=![]() (k>0,x>0)的图象过点B,且AB∥x轴.
(k>0,x>0)的图象过点B,且AB∥x轴.
(1)求a和k的值;
(2)过点B作MN∥OA,交x轴于点M,交y轴于点N,交双曲线y=![]() 于另一点C,求△OBC的面积.
于另一点C,求△OBC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com