
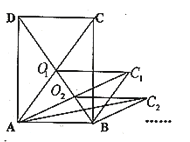
【题目】如图所示,矩形![]() 的面积为
的面积为![]() ,它的两条对角线交于点
,它的两条对角线交于点![]() ,以
,以![]() 、
、![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,平行四边形
,平行四边形![]() 的对角线交于点
的对角线交于点![]() ,同样以
,同样以![]() 、
、![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,……,依次类推,则平行四边形
,……,依次类推,则平行四边形![]() 的面积为( )
的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是正方形,AB=4,点G在BC边上,BG=3,DE⊥AG于点E,BF⊥AG于点F.
(1)求BF和DE的长;
(2)如图2,连接DF、CE,探究并证明线段DF与CE的数量关系与位置关系.


查看答案和解析>>
科目:初中数学 来源: 题型:
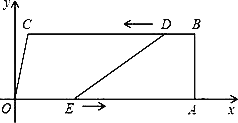
【题目】如图,在四边形OABC中,OA∥BC,∠OAB=90°,O为原点,点C的坐标为(2,8),点A的坐标为(26,0),点D从点B出发,以每秒1个单位长度的速度沿BC向点C运动,点E同时从点O出发,以每秒3个单位长度的速度沿折线OAB运动,当点E达到点B时,点D也停止运动,从运动开始,设D(E)点运动的时间为t秒.
(1)当t为何值时,四边形ABDE是矩形;
(2)当t为何值时,DE=CO?
(3)连接AD,记△ADE的面积为S,求S与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明去文具用品商店给同学买某品牌水性笔,已知甲、乙两商店都有该品牌的水性笔,标价都是2元/支,但甲、乙两商店的优惠条件却不同.
甲商店:若购买不超过10支,则按标价付款;若一次购10支以上,则超过10支的部分按标价的60%付款.
乙商店:按标价的80%付款
在水性笔的质量等因素相同的条件下:
(1)设小明要购买的该品牌笔数是x(x>10)支,则甲商店购买水性笔的费用为 元;乙商店购买水性笔的费用为 元;(用含x的代数式表示,并化简.)
(2)若小明要购买该品牌笔30支,你认为在甲、乙两商店中,到哪个商店购买比较省钱?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
(1)EA是∠QED的平分线;
(2)EF2=BE2+DF2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下表(注:水费按月份结算,![]() 表示立方米).
表示立方米).
每月用水量 | 单价 |
不超过 | 2元/ |
超出 | 4元/ |
超出 | 8元/ |
请根据上表的内容解答下列问题:
(1)若某户居民2月份用水![]() ,则应收水费_________.元
,则应收水费_________.元
(2)若该户居民3月份用水![]() (其中
(其中![]() ),则应收水费多少元(用含a的代数式表示,并简化).
),则应收水费多少元(用含a的代数式表示,并简化).
(3)若该户居民4,5两个月共用水![]() (5月份用水量超过了4月份),设4月份,用水
(5月份用水量超过了4月份),设4月份,用水![]() ,则该户居民4,5两个月共交水费多少元(用含x的代数式表示,并简化).
,则该户居民4,5两个月共交水费多少元(用含x的代数式表示,并简化).
查看答案和解析>>
科目:初中数学 来源: 题型:
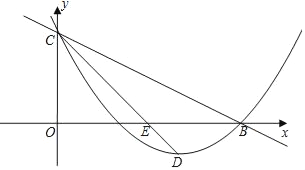
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2﹣2x+c与直线y=﹣![]() x+3分别交于x轴、y轴上的B、C两点,抛物线的顶点为点D,联结CD交x轴于点E.
x+3分别交于x轴、y轴上的B、C两点,抛物线的顶点为点D,联结CD交x轴于点E.
(1)求抛物线的解析式以及点D的坐标;
(2)求tan∠BCD;
(3)点P在直线BC上,若∠PEB=∠BCD,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com