
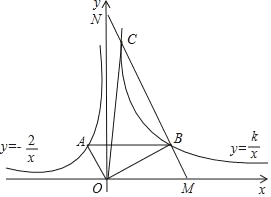
【题目】如图,∠AOB=90°,反比例函数y=﹣![]() (x<0)的图象过点A(﹣1,a),反比例函数y=
(x<0)的图象过点A(﹣1,a),反比例函数y=![]() (k>0,x>0)的图象过点B,且AB∥x轴.
(k>0,x>0)的图象过点B,且AB∥x轴.
(1)求a和k的值;
(2)过点B作MN∥OA,交x轴于点M,交y轴于点N,交双曲线y=![]() 于另一点C,求△OBC的面积.
于另一点C,求△OBC的面积.
【答案】(1)a=2,k=8(2)![]() =15.
=15.
【解析】分析:(1)把A(-1,a)代入反比例函数![]() 得到A(-1,2),过A作AE⊥x轴于E,BF⊥x轴于F,根据相似三角形的性质得到B(4,2),于是得到k=4×2=8;
得到A(-1,2),过A作AE⊥x轴于E,BF⊥x轴于F,根据相似三角形的性质得到B(4,2),于是得到k=4×2=8;
(2)求的直线AO的解析式为y=-2x,设直线MN的解析式为y=-2x+b,得到直线MN的解析式为y=-2x+10,解方程组得到C(1,8),于是得到结论.
详解:(1)∵反比例函数y=﹣![]() (x<0)的图象过点A(﹣1,a),
(x<0)的图象过点A(﹣1,a),
∴a=﹣![]() =2,
=2,
∴A(﹣1,2),
过A作AE⊥x轴于E,BF⊥⊥x轴于F,
∴AE=2,OE=1,
∵AB∥x轴,
∴BF=2,
∵∠AOB=90°,
∴∠EAO+∠AOE=∠AOE+∠BOF=90°,
∴∠EAO=∠BOF,
∴△AEO∽△OFB,
∴![]() ,
,
∴OF=4,
∴B(4,2),
∴k=4×2=8;
(2)∵直线OA过A(﹣1,2),
∴直线AO的解析式为y=﹣2x,
∵MN∥OA,
∴设直线MN的解析式为y=﹣2x+b,
∴2=﹣2×4+b,
∴b=10,
∴直线MN的解析式为y=﹣2x+10,
∵直线MN交x轴于点M,交y轴于点N,
∴M(5,0),N(0,10),
解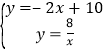 得,
得,![]() ,
,
∴C(1,8),
∴△OBC的面积=S△OMN﹣S△OCN﹣S△OBM=![]() 5×10﹣
5×10﹣![]() ×10×1﹣
×10×1﹣![]() ×5×2=15.
×5×2=15.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
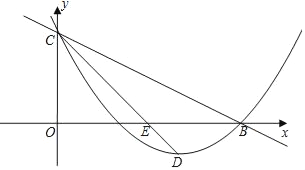
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2﹣2x+c与直线y=﹣![]() x+3分别交于x轴、y轴上的B、C两点,抛物线的顶点为点D,联结CD交x轴于点E.
x+3分别交于x轴、y轴上的B、C两点,抛物线的顶点为点D,联结CD交x轴于点E.
(1)求抛物线的解析式以及点D的坐标;
(2)求tan∠BCD;
(3)点P在直线BC上,若∠PEB=∠BCD,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级两个班,各选派10名学生参加学校举行的“诗词大赛”预赛.参赛选手的成绩如下(单位:分)
九(1)班:88,91,92,93,93,93,94,98,99,100
九(2)班:89,93,93,93,95,96,96,96,98,99.
(1)九(2)班的平均分是 分;九(1)班的众数是 分;
(2)若从两个班成绩最高的5位同学中选2人参加市级比赛,则这两个人来自不同班级的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=4![]() ,则△CEF的周长为_____.
,则△CEF的周长为_____.
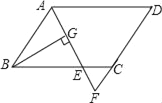
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B,C重合的一个动点,把△EBF沿EF折叠,点B落在B′处.若△CDB′恰为等腰三角形,则DB′的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距离是2![]() ;③tan∠DCF=
;③tan∠DCF=![]() ;④△ABF的面积为
;④△ABF的面积为![]() .其中一定成立的有几个( )
.其中一定成立的有几个( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A点坐标为(5,0),直线y=kx+b(b>0)与y轴交于点B,∠BCA=60°,连接AB,∠α=105°,则直线y=kx+b的表达式为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,D为⊙O上一点,以AD为斜边作△ADC,使∠C=90°,∠CAD=∠DAB
(1)求证:DC是⊙O的切线;
(2)若AB=9,AD=6,求DC的长.
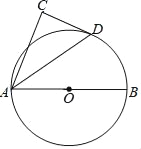
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 一个游戏的中奖概率是![]() ,则做10次这样的游戏一定会中奖
,则做10次这样的游戏一定会中奖
B. 为了解全国中学生的心理健康情况,应该采用普查的方式
C. 一组数据6,8,7,8,8,9,10的众数和中位数都是8
D. 若甲组数据的方差![]() ,乙组数据的方差
,乙组数据的方差![]() ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com