
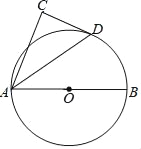
【题目】如图,AB为⊙O的直径,D为⊙O上一点,以AD为斜边作△ADC,使∠C=90°,∠CAD=∠DAB
(1)求证:DC是⊙O的切线;
(2)若AB=9,AD=6,求DC的长.
【答案】(1)见解析;(2)![]()
【解析】分析:
(1)如下图,连接OD,由OA=OD可得∠DAO=∠ADO,结合∠CAD=∠DAB,可得∠CAD=∠ADO,从而可得OD∥AC,由此可得∠C+∠CDO=180°,结合∠C=90°可得∠CDO=90°即可证得CD是⊙O的切线;
(2)如下图,连接BD,由AB是⊙O的直径可得∠ADB=90°=∠C,结合∠CAD=∠DAB可得△ACD∽△ADB,由此可得![]() ,在Rt△ABD中由AD=6,AB=9易得BD=
,在Rt△ABD中由AD=6,AB=9易得BD=![]() ,由此即可解得CD的长了.
,由此即可解得CD的长了.
详解:
(1)如下图,连接OD.
∵OA=OD,
∴∠DAB=∠ODA,
∵∠CAD=∠DAB,
∴∠ODA=∠CAD
∴AC∥OD
∴∠C+∠ODC=180°
∵∠C=90°
∴∠ODC=90°
∴OD⊥CD,
∴CD是⊙O的切线.
(2)如下图,连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∵AB=9,AD=6,
∴BD=![]() =
=![]() =3
=3![]() ,
,
∵∠CAD=∠BAD,∠C=∠ADB=90°,
∴△ACD∽△ADB,
∴![]() ,
,
∴![]() ,
,
∴CD=![]() .
.



科目:初中数学 来源: 题型:
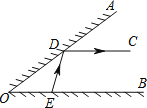
【题目】如图,△AOB的边OA半面镜.∠AOB=36°,在OB边上有点E,从点E射出一束光线经平面镜反射后,反射光线DC恰好满足DC∥OB,已知入射光线、反射光线与半面镜的夹角相等,即∠ODE=∠ADC,求∠DEB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
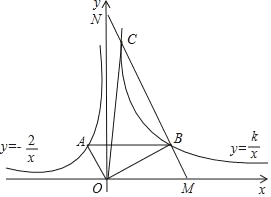
【题目】如图,∠AOB=90°,反比例函数y=﹣![]() (x<0)的图象过点A(﹣1,a),反比例函数y=
(x<0)的图象过点A(﹣1,a),反比例函数y=![]() (k>0,x>0)的图象过点B,且AB∥x轴.
(k>0,x>0)的图象过点B,且AB∥x轴.
(1)求a和k的值;
(2)过点B作MN∥OA,交x轴于点M,交y轴于点N,交双曲线y=![]() 于另一点C,求△OBC的面积.
于另一点C,求△OBC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明过程:
如图,AB∥CD,AD∥BC,BE平分∠ABC,DF平分∠ADC.
求证:BE∥DF.

证明:∵AB∥CD,(已知)
∴∠ABC+∠C=180°.( )
又∵AD∥BC,(已知)
∴ +∠C=180°.( )
∴∠ABC=∠ADC.( )
∵BE平分∠ABC,(已知)
∴∠1=![]() ∠ABC.( )
∠ABC.( )
同理,∠2=![]() ∠ADC.
∠ADC.
∴ =∠2.
∵AD∥BC,(已知)
∴∠2=∠3.( )
∴∠1=∠3,
∴BE∥DF.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
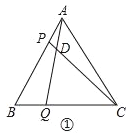
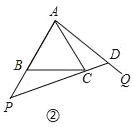
【题目】边长为6的等边△ABC中,点P从点A出发沿射线AB方向移动,同时点Q从点B出发,以相同的速度沿射线BC方向移动,连接AQ、CP,直线AQ、CP相交于点D.
(1)如图①,当点P、Q分别在边AB、BC上时,
①连接PQ,当△BPQ是直角三角形时,AP等于_____;
②∠CDQ的大小是否随P,Q的运动而变化?如果不会,请求出∠CDQ的度数;如果会,请说明理由;
(2)当P、Q分别在边AB、BC的延长线上时,在图②中画出点D,并直接写出∠CDQ的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣4ax+1
(1)写出二次函数图象的对称轴:_____;
(2)如图,设该函数图象交x轴于点A、B(B在A的右侧),交y轴于点C.直线y=kx+b经过点B、C.
①如果k=﹣![]() ,求a的值
,求a的值
②设点P在抛物线对称轴上,PC+PB的最小值为![]() ,求点P的坐标.
,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据路透社报道,中国华为技术有限公司推出新的服务器芯片组,此举正值中国努力提高芯片制造能力,并减少对进口芯片的严重依赖.华为表示,其最新的7纳米64核中央处理器(CPU)将为数据中心提供更高的计算性能并降低功耗.我们知道,1纳米=0.000 000 001米,那么7纳米用科学记数法应记为( )
A.0.7×10![]() 米B.7×10
米B.7×10![]() 米C.7×10
米C.7×10![]() 米D.7×10
米D.7×10![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 a、b、c 在数轴上的位置如图:
![]()
(1)用“<”或“>”填空:a1 0; cb 0; b1 0;
(2)化简:![]() ;
;
(3)若abc0,且b与1的距离和c与1的距离相等,求下列式子的值:2b c (a 4c b).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com