
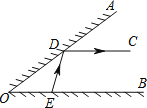
【题目】如图,△AOB的边OA半面镜.∠AOB=36°,在OB边上有点E,从点E射出一束光线经平面镜反射后,反射光线DC恰好满足DC∥OB,已知入射光线、反射光线与半面镜的夹角相等,即∠ODE=∠ADC,求∠DEB的度数.
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下表(注:水费按月份结算,![]() 表示立方米).
表示立方米).
每月用水量 | 单价 |
不超过 | 2元/ |
超出 | 4元/ |
超出 | 8元/ |
请根据上表的内容解答下列问题:
(1)若某户居民2月份用水![]() ,则应收水费_________.元
,则应收水费_________.元
(2)若该户居民3月份用水![]() (其中
(其中![]() ),则应收水费多少元(用含a的代数式表示,并简化).
),则应收水费多少元(用含a的代数式表示,并简化).
(3)若该户居民4,5两个月共用水![]() (5月份用水量超过了4月份),设4月份,用水
(5月份用水量超过了4月份),设4月份,用水![]() ,则该户居民4,5两个月共交水费多少元(用含x的代数式表示,并简化).
,则该户居民4,5两个月共交水费多少元(用含x的代数式表示,并简化).
查看答案和解析>>
科目:初中数学 来源: 题型:
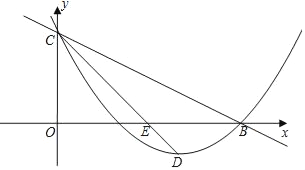
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2﹣2x+c与直线y=﹣![]() x+3分别交于x轴、y轴上的B、C两点,抛物线的顶点为点D,联结CD交x轴于点E.
x+3分别交于x轴、y轴上的B、C两点,抛物线的顶点为点D,联结CD交x轴于点E.
(1)求抛物线的解析式以及点D的坐标;
(2)求tan∠BCD;
(3)点P在直线BC上,若∠PEB=∠BCD,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.
(1)求∠AOE的度数;
(2)若OF平分∠BOE,问:OB是∠DOF的平分线吗?试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小正方形卡片(如图1)不重叠地放在一个底面为长方形(长为mcm,宽为ncm)的盒子的底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.则图2中两块阴影部分的周长和是( )

A. 4mcmB. 4ncmC. 2(m+n)cmD. 4(mn)cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:我国数学家华罗庚在一次出国访问途中,看到飞机上:邻座的乘客阅读的杂志上有一道智力题,求59319的立方根,华罗庚脱口而击.众人惊命,忙问计算奥妙.你知道怎样迅速准确地计算出结果的吗?诺按照下面的分析试一试
(1)由103=1000,1003=100000,可知![]() 是 位数;
是 位数;
(2)由59319的个位数是9,可知![]() 的个位数是 ;
的个位数是 ;
(3)如果划去59319后面的三位319得到59,而33=27,43=64,由此确定![]() 的十位数是 .
的十位数是 .
请应用以上方法计算:![]() = .
= . ![]() =
=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级两个班,各选派10名学生参加学校举行的“诗词大赛”预赛.参赛选手的成绩如下(单位:分)
九(1)班:88,91,92,93,93,93,94,98,99,100
九(2)班:89,93,93,93,95,96,96,96,98,99.
(1)九(2)班的平均分是 分;九(1)班的众数是 分;
(2)若从两个班成绩最高的5位同学中选2人参加市级比赛,则这两个人来自不同班级的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
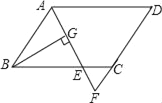
【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=4![]() ,则△CEF的周长为_____.
,则△CEF的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
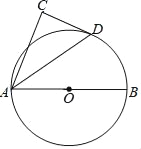
【题目】如图,AB为⊙O的直径,D为⊙O上一点,以AD为斜边作△ADC,使∠C=90°,∠CAD=∠DAB
(1)求证:DC是⊙O的切线;
(2)若AB=9,AD=6,求DC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com