
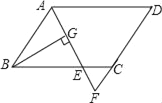
【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=4![]() ,则△CEF的周长为_____.
,则△CEF的周长为_____.
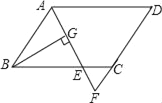
【答案】8
【解析】分析:由AD∥BC,AE平分∠BAD可得∠BAE=∠BEA,则∠CEF=∠F,故AB=BE=6,CF=3.由BE=6,![]() 可得AG=EG=2,由△ABE∽△CFE可求EF.
可得AG=EG=2,由△ABE∽△CFE可求EF.
详解:∵在ABCD中,AB=CD=6,AD=BC=9,∠BAD的平分线交BC于点E,
∴∠BAF=∠DAF,
∵AB∥DF,
∴∠BAF=∠F,
∴∠F=∠DAF,
∴△ADF是等腰三角形,AD=DF=9;
∵AD∥BC,
∴△EFC是等腰三角形,且FC=CE.
∴EC=FC=9﹣6=3,
∴AB=BE.
∴在△ABG中,BG⊥AE,AB=6,BG=![]() ,
,
可得:AG=2,
又∵BG⊥AE,
∴AE=2AG=4,
∴△ABE的周长等于16,
又∵ABCD,
∴△CEF∽△BEA,相似比为1:2,
∴△CEF的周长为8.
故答案为8.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】李师傅在某加工厂工作,厂里规定每个工人平均每天生产零件40个,一周7天生产280个,但由于种种原因,实际每天生产个数与计划相比有出入.下表是李师傅某周的生产情况(超产记为正、减产记为负):

(1)根据记录的数据可知李师傅星期四生产零件______个.
(2)根据记录的数据可知李师傅本周实际生产零件______个.
(3)该厂实行“每周计件工资制”.每生产一个零件可得工资10元,若超额完成任务,则超过部分每个另奖5元;少生产一个则倒扣3元,那么李师傅这一周的工资总额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
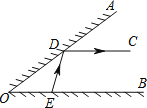
【题目】如图,△AOB的边OA半面镜.∠AOB=36°,在OB边上有点E,从点E射出一束光线经平面镜反射后,反射光线DC恰好满足DC∥OB,已知入射光线、反射光线与半面镜的夹角相等,即∠ODE=∠ADC,求∠DEB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两块完全相同的直角三角形纸片的直角顶点![]() 叠放在一起,若保持
叠放在一起,若保持![]() 不动,将
不动,将![]() 绕直角顶点
绕直角顶点![]() 旋转.
旋转.
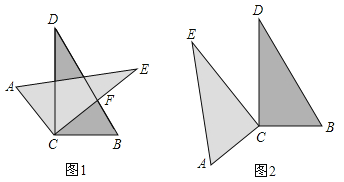
(1)当![]() 绕直角顶点
绕直角顶点![]() 旋转到如图1的位置时,
旋转到如图1的位置时,
①若![]() ,则
,则![]() =_________°;若
=_________°;若![]() ,则
,则![]() =_________°;
=_________°;
②猜想![]() 与
与![]() 的数量关系为:_________;
的数量关系为:_________;
(2)当![]() 绕直角顶点
绕直角顶点![]() 旋转到如图2的位置时,②中
旋转到如图2的位置时,②中![]() 与
与![]() 的数量关系是否仍然成立?请说明理由.(注:
的数量关系是否仍然成立?请说明理由.(注:![]() 与
与![]() 为小于平角的角)
为小于平角的角)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 两地相距300
两地相距300![]() ,甲、乙两车同时从
,甲、乙两车同时从![]() 地出发驶向
地出发驶向![]() 地,甲车到达
地,甲车到达![]() 地后立即返回,如图是两车离
地后立即返回,如图是两车离![]() 地的距离
地的距离![]() (
(![]() )与行驶时间
)与行驶时间![]() (
(![]() )之间的函数图象.
)之间的函数图象.
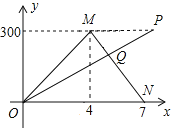
(1)求甲车行驶过程中![]() 与
与![]() 之间的函数解析式,并写出自变量
之间的函数解析式,并写出自变量![]() 的取值范围.
的取值范围.
(2)若两车行驶5![]() 相遇,求乙车的速度.
相遇,求乙车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
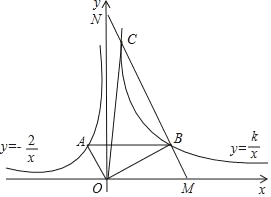
【题目】如图,∠AOB=90°,反比例函数y=﹣![]() (x<0)的图象过点A(﹣1,a),反比例函数y=
(x<0)的图象过点A(﹣1,a),反比例函数y=![]() (k>0,x>0)的图象过点B,且AB∥x轴.
(k>0,x>0)的图象过点B,且AB∥x轴.
(1)求a和k的值;
(2)过点B作MN∥OA,交x轴于点M,交y轴于点N,交双曲线y=![]() 于另一点C,求△OBC的面积.
于另一点C,求△OBC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据路透社报道,中国华为技术有限公司推出新的服务器芯片组,此举正值中国努力提高芯片制造能力,并减少对进口芯片的严重依赖.华为表示,其最新的7纳米64核中央处理器(CPU)将为数据中心提供更高的计算性能并降低功耗.我们知道,1纳米=0.000 000 001米,那么7纳米用科学记数法应记为( )
A.0.7×10![]() 米B.7×10
米B.7×10![]() 米C.7×10
米C.7×10![]() 米D.7×10
米D.7×10![]() 米
米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com