
【题目】在平面直角坐标系中,我们定义直线y=ax﹣a为抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
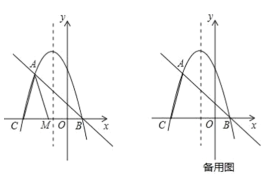
已知抛物线![]() 与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
(1)填空:该抛物线的“梦想直线”的解析式为 ,
(2)如图,点M为线段CB上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“梦想三角形”,求点N的坐标;
(3)当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x+
x+![]() (2)N点坐标为(0,2
(2)N点坐标为(0,2![]() 3)或(
3)或(![]() ,
,![]() )(3)满足条件的点F,此时E(1,
)(3)满足条件的点F,此时E(1,![]() )、F(0,
)、F(0,![]() )或E(1,
)或E(1,![]() ),F(4,
),F(4,![]() ).
).
【解析】
(1)由梦想直线的定义可求得其解析式;
(2)当N点在y轴上时,过A作AD⊥y轴于点D,则可知AN=AC,结合A点坐标,则可求得ON的长,可求得N点坐标;当M点在y轴上即,M点在原点时,过N作NP⊥x轴于点P,由条件可求得∠NMP=60°,在Rt△NMP中,可求得MP和NP的长,则可求得N点坐标;
(3)当AC为平行四边形的一边时,过F作对称轴的垂线FH,过A作AK⊥x轴于点K,可证△EFH≌△ACK,可求得DF的长,则可求得F点的横坐标,从而可求得F点坐标,由HE的长可求得E点坐标;当AC为平行四边形的对角线时,设E(1,t),由A、C的坐标可表示出AC中点,从而可表示出F点的坐标,代入直线AB的解析式可求得t的值,可求得E、F的坐标.
(1)∵抛物线![]() ,
,
∴其梦想直线的解析式为y=![]() x+
x+![]()
故答案为:y=![]() x+
x+![]() ;
;
(2)联立梦想直线与抛物线解析式可得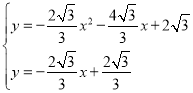 ,
,
解得 或
或![]() ,
,
∴A(2,2![]() ),B(1,/span>0),
),B(1,/span>0),
当点N在y轴上时,△AMN为梦想三角形,
如图1,过A作AD⊥y轴于点D,则AD=2,
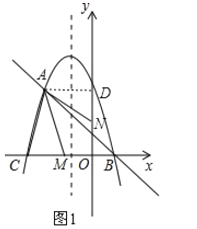
在![]() 中,令y=0可求得x=3或x=1,
中,令y=0可求得x=3或x=1,
∴C(3,0),且A(2,2![]() ),
),
∴AC=![]() ,
,
由翻折的性质可知AN=AC=![]() ,
,
在Rt△AND中,由勾股定理可得DN=![]() =
=![]() =3,
=3,
∵OD=2![]() ,
,
∴ON=2![]() 3或ON=2
3或ON=2![]() +3,
+3,
当ON=2![]() +3时,则MN>OD>CM,与MN=CM矛盾,不合题意,
+3时,则MN>OD>CM,与MN=CM矛盾,不合题意,
∴N点坐标为(0,2![]() 3);
3);
当M点在y轴上时,则M与O重合,过N作NP⊥x轴于点P,如图2,
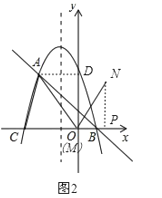
在Rt△AMD中,AD=2,OD=2![]() ,
,
∴tan∠DAM=![]() =3,
=3,
∴∠DAM=60°,
∵AD∥x轴,
∴∠AMC=∠DAO=60°,
又由折叠可知∠NMA=∠AMC=60°,
∴∠NMP=60°,且MN=CM=3,
∴MP=![]() MN=
MN=![]() ,NP=MNsin60°=
,NP=MNsin60°=![]()
![]() ,
,
∴此时N点坐标为(![]() ,
,![]() );
);
综上可知N点坐标为(0,2![]() 3)或(
3)或(![]() ,
,![]() );
);
(3)①当AC为平行四边形的边时,如图2,过F作对称轴的垂线FH,过A作AK⊥x轴于点K,

则有AC∥EF且AC=EF,
∴∠ACK=∠EFH,
在△ACK和△EFH中

∴△ACK≌△EFH(AAS),
∴FH=CK=1,HE=AK=2![]() ,
,
∵抛物线对称轴为x=1,
∴F点的横坐标为0或2,
∵点F在直线AB上,
∴当F点横坐标为0时,则F(0,![]() ),此时点E在直线AB下方,
),此时点E在直线AB下方,
∴E到x轴的距离为EHOF=2![]()
![]() =
=![]() ,即E点纵坐标为
,即E点纵坐标为![]() ,
,
∴E(1,![]() );
);
当F点的横坐标为2时,则F与A重合,不合题意,舍去;
②当AC为平行四边形的对角线时,
∵C(3,0),且A(2,2![]() ),
),
∴线段AC的中点坐标为(2.5,![]() ),
),
设E(1,t),F(x,y),
则x1=2×(2.5),y+t=2![]() ,
,
∴x=4,y=2![]() t,
t,
代入直线AB解析式可得2![]() t=
t=![]() ×(4)+
×(4)+![]() ,解得t=
,解得t=![]() ,
,
∴E(1,![]() ),F(4,
),F(4,![]() );
);
综上可知存在满足条件的点F,此时E(1,![]() )、F(0,
)、F(0,![]() )或E(1,
)或E(1,![]() ),F(4,
),F(4,![]() ).
).


科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的对角线AC,BD相交于点O.
(1)如图1,E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OE=OG;
(2)如图2,H是BC上的点,过点H作EH⊥BC,交线段OB于点E,连结DH交CE于点F,交OC于点G.若OE=OG,
①求证:∠ODG=∠OCE;
②当AB=1时,求HC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
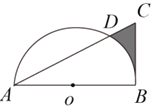
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=![]() ,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )
,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“每天锻炼一小时,健康生活一辈子”,学校准备从小明和小亮2人中随机选拔一人当“阳光大课间”领操员,体育老师设计的游戏规则是:将四张扑克牌(方块2、黑桃4、黑桃5、梅花5)的牌面如图1,扑克牌洗匀后,如图2背面朝上放置在桌面上.小亮和小明两人各抽取一张扑克牌,两张牌面数字之和为奇数时,小亮当选;否则小明当选.

(1)请用树状图或列表法求出所有可能的结果;
(2)请问这个游戏规则公平吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017江西省)如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直.
(1)若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;
(2)若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°?
(参考数据:sin69°≈![]() ,cos21°≈
,cos21°≈![]() ,tan20°≈
,tan20°≈![]() ,tan43°≈
,tan43°≈![]() ,所有结果精确到个位)
,所有结果精确到个位)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴,
轴,![]() 轴交于
轴交于![]() ,
,![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() ,
,![]() .
.

(1)求![]() 的值;
的值;
(2)求出直线![]() 的解析式;
的解析式;
(3)![]() 为线段
为线段![]() 上一点(不含端点),连接
上一点(不含端点),连接![]() ,一动点
,一动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 以每秒1个单位长度的速度运动到
以每秒1个单位长度的速度运动到![]() ,再沿线段
,再沿线段![]() 以每秒
以每秒![]() 个单位长度的速度运动到点
个单位长度的速度运动到点![]() 后停止,请直接写出点
后停止,请直接写出点![]() 在整个运动过程的最少用时.(提示:过点
在整个运动过程的最少用时.(提示:过点![]() 和点
和点![]() ,分别作
,分别作![]() 轴,
轴,![]() 轴的垂线
轴的垂线![]() ,
,![]() ,两垂线交于点
,两垂线交于点![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,
中,![]() ,
,![]() 是
是![]() 边的中点,点
边的中点,点![]() 是正方形内一动点,
是正方形内一动点,![]() ,连接
,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得
得![]() ,连接
,连接![]() ,
,![]() .
.
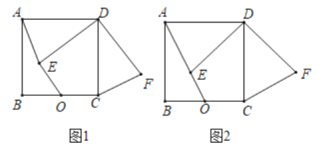
(1)如图1,求证:![]() ;
;
(2)如图2,若![]() ,
,![]() ,
,![]() 三点共线,求点
三点共线,求点![]() 到直线
到直线![]() 的距离.
的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
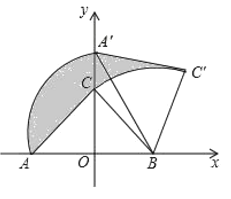
【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的点A'处,若AO=OB=2,则图中阴影部分面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的“文明出行”知识竞赛中,8(1)和8(2)班参赛人数相同,成绩分为A、B、C三个等级,其中相应等级的得分依次记为A级100分、B级90分、C级80分,达到B级以上(含B级)为优秀,其中8(2)班有2人达到A级,将两个班的成绩整理并绘制成如下的统计图,请解答下列问题:

(1)求各班参赛人数,并补全条形统计图;
(2)此次竞赛中8(2)班成绩为C级的人数为_______人;
(3)小明同学根据以上信息制作了如下统计表:
平均数(分) | 中位数(分) | 方差 | |
8(1)班 | m | 90 | n |
8(2)班 | 91 | 90 | 29 |
请分别求出m和n的值,并从优秀率和稳定性方面比较两个班的成绩;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com