
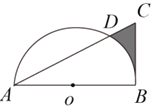
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=![]() ,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )
,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
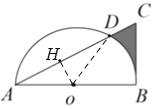
连接OD,过点O作OH⊥AC,垂足为 H,则有AD=2AH,∠AHO=90°,在Rt△ABC中,利用∠A的正切值求出∠A=30°,继而可求得OH、AH长,根据圆周角定理可求得∠BOC =60°,然后根据S阴影=S△ABC-S△AOD-S扇形BOD进行计算即可.
连接OD,过点O作OH⊥AC,垂足为 H,
则有AD=2AH,∠AHO=90°,
在Rt△ABC中,∠ABC=90°,AB=![]() ,BC=2,tan∠A=
,BC=2,tan∠A=![]() ,
,
∴∠A=30°,
∴OH=![]() OA=
OA=![]() ,AH=AOcos∠A=
,AH=AOcos∠A=![]() ,∠BOC=2∠A=60°,
,∠BOC=2∠A=60°,
∴AD=2AH=![]() ,
,
∴S阴影=S△ABC-S△AOD-S扇形BOD=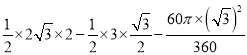 =
=![]() ,
,
故选A.


科目:初中数学 来源: 题型:
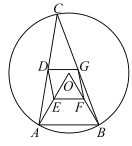
【题目】如图,![]() 是半径为4的
是半径为4的![]() 的内接三角形,连接
的内接三角形,连接![]() ,点
,点![]() 分别是
分别是![]() 的中点.
的中点.
(1)试判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(2)填空:①若![]() ,当
,当![]() 时,四边形
时,四边形![]() 的面积是__________;②若
的面积是__________;②若![]() ,当
,当![]() 的度数为__________时,四边形
的度数为__________时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的边长为5,E在BC边上运动,DE的中点G,EG绕E顺时针旋转90°得EF,问CE为多少时A、C、F在一条直线上( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC(AC<AB<BC),请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
(1)在边BC上确定一点P,使得PA+PC=BC;
(2)作出一个△DEF,使得:①△DEF是直角三角形;②△DEF的周长等于边BC的长。
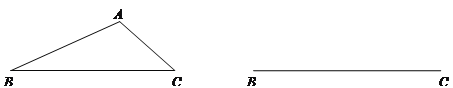
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校团委为了教育学生,开展了以感恩为主题的有奖征文活动,并为获奖的同学颁发奖品.小红与小明去文化商店购买甲、乙两种笔记本作为奖品,若买甲种笔记本20个,乙种笔记本10个,共用110元;且买甲种笔记本30个比买乙种笔记本20个少花10元.
(1)求甲、乙两种笔记本的单价各是多少元?
(2)若本次购进甲种笔记本的数量比乙种笔记本的数量的2倍还少10个,且购进两种笔记本的总数量不少于80本,总金额不超过320元.请你设计出本次购进甲、乙两种笔记本的所有方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠CAB=90°,AB=AC,点A在y轴上,BC∥x轴,点B![]() .将△ABC绕点A顺时针旋转的△AB′C′,当点B′落在x轴的正半轴上时,点C′的坐标为( )
.将△ABC绕点A顺时针旋转的△AB′C′,当点B′落在x轴的正半轴上时,点C′的坐标为( )
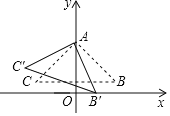
A.(﹣![]() ,
,![]() ﹣1)B.(﹣
﹣1)B.(﹣![]() ,
,![]() ﹣1)
﹣1)
C.(﹣![]() ,
,![]() +1)D.(﹣
+1)D.(﹣![]() ,
,![]() ﹣1)
﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们定义直线y=ax﹣a为抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
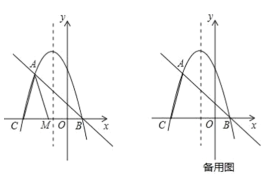
已知抛物线![]() 与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
(1)填空:该抛物线的“梦想直线”的解析式为 ,
(2)如图,点M为线段CB上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“梦想三角形”,求点N的坐标;
(3)当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E,F分别在边AD,DC上,AB=6,DF=4,将矩形沿直线EF折叠,点D恰好落在BC边上的点G处,连接DG交EF于点H.
(1)求DE的长度.
(2)求![]() 的值.
的值.
(3)若AB边上有且只存在2个点P,使△APE与△BPG相似,请直接写出边AD的值.
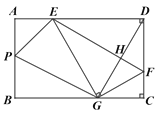
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com