
【题目】如图,抛物线![]() 与
与![]() 轴交于点A和点B(3,0),与
轴交于点A和点B(3,0),与![]() 轴交于点C(0,3).
轴交于点C(0,3).
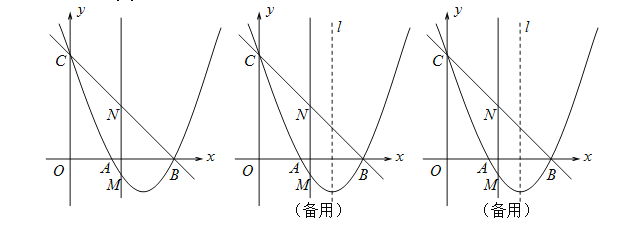
(1)求抛物线的解析式;
(2)若点M是抛物线在![]() 轴下方上的动点,过点M作MN//
轴下方上的动点,过点M作MN//![]() 轴交直线BC于点N,求线段MN的最大值;
轴交直线BC于点N,求线段MN的最大值;
(3)在(2)的条件下,当MN取最大值时,在抛物线的对称轴![]() 上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)(2,
;(3)(2,![]() )、(2,
)、(2,![]() )、(2,
)、(2,![]() )、(2,
)、(2,![]() )或(2,
)或(2,![]() ).
).
【解析】
试题分析:(1)由点B、C的坐标利用待定系数法即可求出抛物线的解析式;
(2)设出点M的坐标以及直线BC的解析式,由点B、C的坐标利用待定系数法即可求出直线BC的解析式,结合点M的坐标即可得出点N的坐标,由此即可得出线段MN的长度关于m的函数关系式,再结合点M在x轴下方可找出m的取值范围,利用二次函数的性质即可解决最值问题;
(3)假设存在,设出点P的坐标为(2,n),结合(2)的结论可求出点N的坐标,结合点N、B的坐标利用两点间的距离公式求出线段PN、PB、BN的长度,根据等腰三角形的性质分类讨论即可求出n值,从而得出点P的坐标.
试题解析:(1)将点B(3,0)、C(0,3)代入抛物线![]() 中,得
中,得![]() :,解得:
:,解得:![]() ,∴抛物线的解析式为
,∴抛物线的解析式为![]() ;
;
(2)设点M的坐标为(m,![]() ),设直线BC的解析式为y=kx+3,把点点B(3,0)代入y=kx+3中,得:0=3k+3,解得:k=﹣1,∴直线BC的解析式为y=﹣x+3.∵MN∥y轴,∴点N的坐标为(m,﹣m+3).∵抛物线的解析式为
),设直线BC的解析式为y=kx+3,把点点B(3,0)代入y=kx+3中,得:0=3k+3,解得:k=﹣1,∴直线BC的解析式为y=﹣x+3.∵MN∥y轴,∴点N的坐标为(m,﹣m+3).∵抛物线的解析式为![]() =
=![]() ,∴抛物线的对称轴为x=2,∴点(1,0)在抛物线的图象上,∴1<m<3.∵线段MN=﹣m+3﹣(
,∴抛物线的对称轴为x=2,∴点(1,0)在抛物线的图象上,∴1<m<3.∵线段MN=﹣m+3﹣(![]() )=
)=![]() =
=![]() ,∴当m=
,∴当m=![]() 时,线段MN取最大值,最大值为
时,线段MN取最大值,最大值为![]() ;
;
(3)假设存在.设点P的坐标为(2,n).
当m=![]() 时,点N的坐标为(
时,点N的坐标为(![]() ,
,![]() ),∴PB=
),∴PB=![]() =
=![]() ,PN=
,PN=![]() ,BN=
,BN=![]() =
=![]() .
.
△PBN为等腰三角形分三种情况:
①当PB=PN时,即![]() =
=![]() ,解得:n=
,解得:n=![]() ,此时点P的坐标为(2,
,此时点P的坐标为(2,![]() );
);
②当PB=BN时,即![]() =
=![]() ,解得:n=±
,解得:n=±![]() ,此时点P的坐标为(2,
,此时点P的坐标为(2,![]() )或(2,
)或(2,![]() );
);
③当PN=BN时,即![]() =
=![]() ,解得:n=
,解得:n=![]() ,此时点P的坐标为(2,
,此时点P的坐标为(2,![]() )或(2,
)或(2,![]() ).
).
综上可知:在抛物线的对称轴l上存在点P,使△PBN是等腰三角形,点的坐标为(2,![]() )、(2,
)、(2,![]() )、(2,
)、(2,![]() )、(2,
)、(2,![]() )或(2,
)或(2,![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=mx+n与双曲线y=![]() 相交于A(﹣1,2)、B(2,b)两点,与y轴相交于点C.
相交于A(﹣1,2)、B(2,b)两点,与y轴相交于点C.
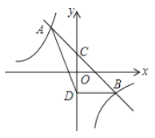
(1)求m,n的值;
(2)若点D与点C关于x轴对称,求△ABD的面积;
(3)在坐标轴上是否存在异于D点的点P,使得S△PAB=S△DAB?若存在,直接写出P点坐标;若不存在,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1:![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)

(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() 1.414,
1.414,![]() 1.732)
1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
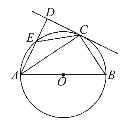
【题目】如图,已知AB是☉O的直径,DC是☉O的切线,点C是切点,AD⊥DC,垂足为D,且与圆O相交于点E.
(1)求证:∠DAC=∠BAC.
(2)若☉O的直径为5cm,EC=3cm,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
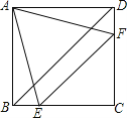
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在BC和CD上,下列结论:①CE=CF;②BD=1+![]() ;③BE+DF=EF;④∠AEB=75°.其中正确的序号是______.
;③BE+DF=EF;④∠AEB=75°.其中正确的序号是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
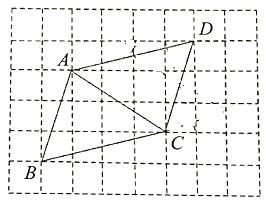
【题目】如图,在所给的方格纸中,每个小正方形的边长都是1,四边形![]() 是平行四边形,连结
是平行四边形,连结![]() (点
(点![]() ,
,![]() ,
,![]() ,
,![]() 均在格点上),请按要求完成下列作图任务.要求:①仅用无刻度直尺,且不能用直尺中的直角;②保留作图痕迹.
均在格点上),请按要求完成下列作图任务.要求:①仅用无刻度直尺,且不能用直尺中的直角;②保留作图痕迹.
(1)在图1中作![]() 的中位线
的中位线![]() ,且
,且![]() ;
;
(2)在图2中取边![]() 上点
上点![]() ,以
,以![]() ,
,![]() 为邻边作
为邻边作![]() ,且
,且![]() 的面积等于
的面积等于![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备购进一批电冰箱和空调,每台电冰箱的进价比每台空调的进价多400元,商店用8000元购进电冰箱的数量与用6400元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)已知电冰箱的销售价为每台2100元,空调的销售价为每台1750元.若商店准备购进这两种家电共100台,其中购进电冰箱x台(33≤x≤40),那么该商店要获得最大利润应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
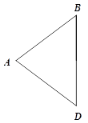
【题目】如图,在△ABD中,∠ABD = ∠ADB,分别以点B,D为圆心,AB长为半径在BD的右侧作弧,两弧交于点C,连接BC,DC和AC,AC与BD交于点O.
(1)用尺规补全图形,并证明四边形ABCD为菱形;
(2)如果AB = 5,![]() ,求BD的长.
,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (
(![]() 是常数,
是常数,![]() )的自变量
)的自变量![]() 与函数值
与函数值![]() 的部分对应值如下表:
的部分对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … |
|
|
|
|
| … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②
;②![]() 和3是关于
和3是关于![]() 的方程
的方程![]() 的两个根;③
的两个根;③![]()
![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com