
分析 (1)根据利润=销售量×(销售单价-成本),代入代数式求出函数关系式;
(2)令利润z=440,求出x的值;
(3)根据厂商每月的制造成本不超过540万元,以及成本价18元,得出销售单价的取值范围,进而得出最大利润.
解答 解:(1)由题意得,z=y(x-18)
=(-2x+100)(x-18)
=-2x2+136x-1800;
(2)当z=440时,
-2x2+136x-1800=440,
解得:x1=28,x2=40.
答:当销售单价为28元或40元时,厂商每月获得的利润为440万元;
(3)∵厂商每月的制造成本不超过540万元,每件制造成本为18元,
∴每月的生产量为:小于等于$\frac{540}{18}$=30万件,
y=-2x+100≤30,
解得:x≥35,
∵z=-2x2+136x-1800=-2(x-34)2+512,
∴图象开口向下,对称轴右侧z随x的增大而减小,
∴x=35时,z最大为:510万元.
当销售单价为35元时,厂商每月获得的利润最大,最大利润为510万元.
点评 本题考查的是二次函数在实际生活中的应用,关键是根据题意求出二次函数的解析式以及利用增减性求出最值.


科目:初中数学 来源: 题型:填空题
 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC.若∠CAB=22.5°,CD=6cm,则⊙O的半径为3$\sqrt{2}$cm.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC.若∠CAB=22.5°,CD=6cm,则⊙O的半径为3$\sqrt{2}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,小“鱼”与大“鱼”是位似图形,如果小“鱼”上一个“顶点”的坐标为(a,-b),那么大“鱼”上对应“顶点”的坐标为(-2a,2b).
如图,小“鱼”与大“鱼”是位似图形,如果小“鱼”上一个“顶点”的坐标为(a,-b),那么大“鱼”上对应“顶点”的坐标为(-2a,2b).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
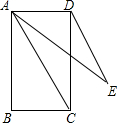 如图,矩形ABCD,AB=2$\sqrt{3}$,AC=4,将对角线AC绕点A旋转得到线段AE,连接DE,DE∥AC,则线段DE=-1+$\sqrt{13}$.
如图,矩形ABCD,AB=2$\sqrt{3}$,AC=4,将对角线AC绕点A旋转得到线段AE,连接DE,DE∥AC,则线段DE=-1+$\sqrt{13}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com