C
分析:由四边形ABCD是菱形,即可得BF为∠ABE的角平分线;可得①正确;由当∠ABC=60°时,DF=2BF,可得②错误;连接AC,易证得△AOD∽△FAD,由相似三角形的对应边成比例,可证得AD:DF=OD:AD,继而可得2AB
2=DF•DB,即④正确;连接FC,易证得△ABF≌△CBF(SAS),可得∠BCF=∠BAE,AF=CF,然后由正弦函数的定义,可求得④正确.
解答:①∵四边形ABCD是菱形,
∴BF为∠ABE的角平分线,
故①正确;
②连接AC交BD于点O,
∵四边形ABCD是菱形,
∴AB=BC=AD,
∴当∠ABC=60°时,△ABC是等边三角形,
即AB=AC,
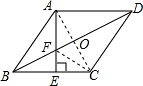
则DF=2BF,
∵∠ABC的度数不定,
∴DF不一定等于2BF;
故②错误;
③∵AE⊥BC,AD∥BC,
∴AE⊥AD,
∴∠FAD=90°,
∵四边形ABCD是菱形,
∴AC⊥BD,OB=OD=

DB,AD=AB,
∴∠AOD=∠FAD=90°,
∵∠ADO=∠FDO,
∴△AOD∽△FAD,
∴AD:DF=OD:AD,
∴AD
2=DF•OD,
∴AB
2=DF•

DB,
即2AB
2=DF•DB;
故③正确;
④连接CF,
在△ABF和△CBF中,
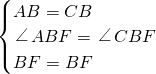
,
∴△ABF≌△CBF(SAS),
∴∠BCF=∠BAE,AF=CF,
在Rt△EFC中,sin∠ECF=
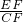
=

,
∴sin∠BAE=

.
故④正确.
故选C.
点评:此题考查了相似三角形的判定与性质、菱形的性质、全等三角形的判定与性质以及锐角三角函数的定义.此题难度较大,注意掌握辅助线的作法,注意数形结合思想的应用.

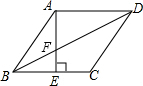 菱形ABCD中,AE⊥BC于E,交BD于F点,下列结论:
菱形ABCD中,AE⊥BC于E,交BD于F点,下列结论: .
.
 DB,AD=AB,
DB,AD=AB, DB,
DB,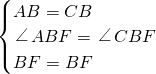 ,
,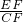 =
= ,
, .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案