
如图,在△ABC中,∠ACB=90°,CD⊥AB于D.把三角形沿AE对折使点C落在AB边上的点F上,CD与折痕AE相交于G,连结FG并延长交AC于H.
(1)判断FH与BC的位置关系,并说明理由;
(2)判断HG与DG的数量关系,并说明理由.
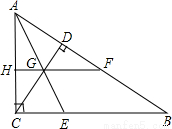
(1)FH∥BC;理由见解析;(2)HG=DG;理由见解析.
【解析】
试题分析:(1)连接EF,根据翻折变换的性质可得∠CAE=∠EAF,∠AFE=90°,CE=EF,根据垂直的定义可得∠ADC=90°,然后根据同位角相等,两直线平行判断出EF∥CD,然后根据等角的余角相等求出∠AGD=∠AEC,再求出∠CGE=∠AEC,根据等角对等边可得CG=CE,然后求出CG=EF,再根据一组对边平行且相等的四边形是平行四边形判断出四边形CEFG是平行四边形,根据平行四边形对边平行可得GF∥CE,即FH∥BC;
(2)根据两直线平行,同位角相等可得∠AHG=∠ACB=90°,再根据角平分线上的点到角的两边距离相等可得HG=DG.
试题解析:(1)【解析】
如图,连接EF,
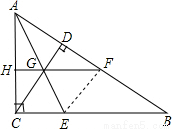
由翻折的性质得,∠CAE=∠EAF,∠AFE=∠ACB=90°,CE=EF,
∵CD⊥AB,
∴∠ADC=90°,
∴∠ADC=∠AFE,
∴EF∥CD,
∵∠CAE=∠EAF,∠CAE+∠AEC=∠EAF+∠AGD=90°,
∴∠AGD=∠AEC,
又∵∠AGD=∠CGE(对顶角相等),
∴∠CGE=∠AEC,
∴CE=CG,
∴CG=EF,
∴四边形CEFG是平行四边形,
∴GF∥CE,
即FH∥BC;
(2)【解析】
∵FH∥BC,
∴∠AHG=∠ACB=90°,
又∵∠CAE=∠EAF,
∴HG=DG.
考点:翻折变换(折叠问题).


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源:2016届北京市通州区七年级下学期期末数学试卷(解析版) 题型:解答题
把下列各式进行因式分【解析】
(1)3ax2-6axy+3ay2;
(2)x2(x-y)+(y-x).
查看答案和解析>>
科目:初中数学 来源:2015届黑龙江省八年级下学期期末考试数学试卷(解析版) 题型:解答题
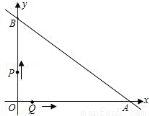
直线y=﹣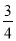 x+6与坐标轴分别交于A、B两点,动点P、Q同时从O点出发,同时到达A点,运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿路线O→B→A运动.
x+6与坐标轴分别交于A、B两点,动点P、Q同时从O点出发,同时到达A点,运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿路线O→B→A运动.
(1)直接写出A、B两点的坐标;
(2)设点Q的运动时间为t(秒),△OPQ的面积为S,求出S与t之间的函数关系式;
(3)当S=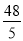 时,求出点P的坐标,并直接写出以点O、P、Q为顶点的平行四边形的第四个顶点M的坐标.
时,求出点P的坐标,并直接写出以点O、P、Q为顶点的平行四边形的第四个顶点M的坐标.
查看答案和解析>>
科目:初中数学 来源:2015届重庆市岩口复兴学校八年级下学期期中命题三数学试卷(解析版) 题型:选择题
已知反比例函数y=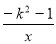 的图象上有三个点(2,
的图象上有三个点(2,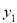 ),(3,
),(3,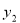 ),(
),(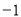 ,
,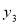 ),则
),则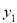 ,
,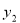 ,
,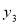 的大小关系是( )
的大小关系是( )
A.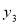 >
>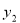 >
>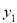 B.
B.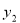 >
>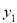 >
>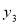
C.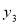 >
>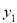 >
>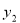 D.
D.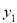 >
>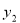 >
>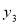
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com