
 交
交 轴于点
轴于点 ,交
,交 轴于点
轴于点 ,抛物线
,抛物线 经过
经过 、
、 、
、 (1,0)三点.
(1,0)三点.
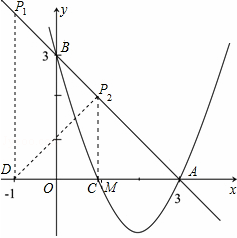
 的坐标为(-1,0),在直线
的坐标为(-1,0),在直线 上有一点
上有一点 ,使
,使 与
与 相似,求出点
相似,求出点 的坐标;
的坐标; 轴下方的抛物线上,是否存在点
轴下方的抛物线上,是否存在点 ,使
,使 的面积等于四边形
的面积等于四边形 的面积?如果存在,请求出点
的面积?如果存在,请求出点 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.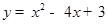 ;(2)
;(2)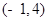 或(1,2);(3)不存在
或(1,2);(3)不存在 与坐标轴的交点A、B的坐标,再由抛物线经过A、B、C三点即可根据待定系数法求得结果;
与坐标轴的交点A、B的坐标,再由抛物线经过A、B、C三点即可根据待定系数法求得结果;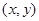 ,根据三角形的面积公式可得
,根据三角形的面积公式可得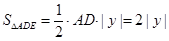 ①当P1(-1,4)时,
①当P1(-1,4)时,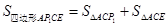
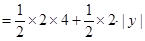 =
= 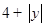 ,由点E在x轴下方可得
,由点E在x轴下方可得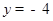 ,代入得
,代入得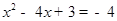 即
即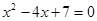 ,根据△=(-4)2-4×7=-12<0可得此方程无解;②当P2(1,2)时,
,根据△=(-4)2-4×7=-12<0可得此方程无解;②当P2(1,2)时,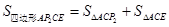 =
= 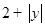 ,由点E在x轴下方可得
,由点E在x轴下方可得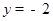 ,代入得:
,代入得: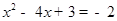 ,即
,即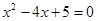 ,根据△=(-4)2-4×5=-4<0可得此方程无解,综上所述,在x轴下方的抛物线上不存在这样的点E.
,根据△=(-4)2-4×5=-4<0可得此方程无解,综上所述,在x轴下方的抛物线上不存在这样的点E.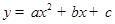 得方程组
得方程组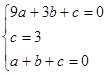 ,解得:
,解得: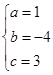
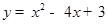 ;
;
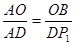
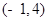
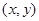 ,则
,则 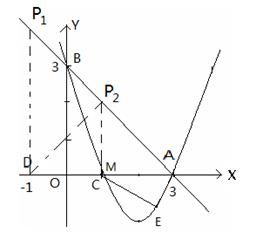
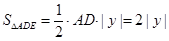
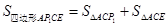
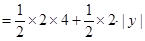 =
= 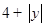
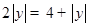 ,
,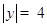
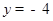 ,代入得
,代入得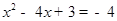 即
即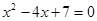
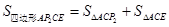 =
= 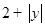
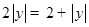 ,
,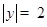
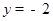 ,代入得:
,代入得: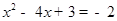 ,即
,即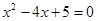 ,
,

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源:不详 题型:解答题
 ,抛物线y=ax2+bx经过点A(4,0)与点(-2,6).
,抛物线y=ax2+bx经过点A(4,0)与点(-2,6).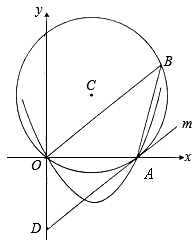
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
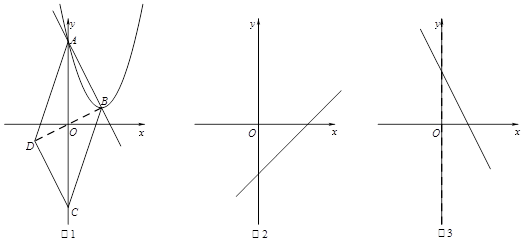
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则
(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则 = .
= . 
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 :
: 上的点,过点P的另一条直线
上的点,过点P的另一条直线 交抛物线
交抛物线 于A、B两点.
于A、B两点.
 的解析式为
的解析式为 ,求A、B两点的坐标;
,求A、B两点的坐标;  ),当PA=AB时,请直接写出点A的坐标;
),当PA=AB时,请直接写出点A的坐标; 上任意给定的一点P,在抛物线上都能找到点A,使得PA=AB成立.
上任意给定的一点P,在抛物线上都能找到点A,使得PA=AB成立. 交
交 轴于点C,若△AOB的外心在边AB上,且∠BPC=∠OCP,求点P的坐标.
轴于点C,若△AOB的外心在边AB上,且∠BPC=∠OCP,求点P的坐标.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (克)与销售时间
(克)与销售时间 (月份)之间的函数图象. (4月份以30天计算)
(月份)之间的函数图象. (4月份以30天计算)
| 商品名称 金 额 | A | B | |||
| 投资金额x(万元) | x | 5 | x | 1 | 5 |
| 销售收入y(万元) | y1=kx (k≠0) | 3 | y2=ax2+bx(a≠0) | 2.8 | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com