
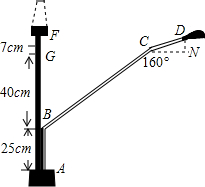
 如图,马路边安装的路灯由支柱上端的钢管ABCD支撑,图中标出了相关的数据,其中CG⊥⊥AF,FD⊥AF,点G、点F分别是垂足,请根据这些信息计算钢管ABCD的长度.(钢管的直径忽略不计.结果精确到1cm.参考数据:sinθ≈0.17,cos10°≈0.98,tan10°≈0.18,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
如图,马路边安装的路灯由支柱上端的钢管ABCD支撑,图中标出了相关的数据,其中CG⊥⊥AF,FD⊥AF,点G、点F分别是垂足,请根据这些信息计算钢管ABCD的长度.(钢管的直径忽略不计.结果精确到1cm.参考数据:sinθ≈0.17,cos10°≈0.98,tan10°≈0.18,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36) 分析 连接CG,DF,分别求出BC,CD的长,即可求出钢管ABCD的长度.
解答 解:
连接CG,DF,由题意可知CG⊥⊥AF,FD⊥AF,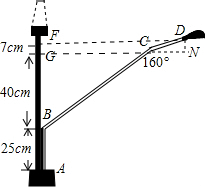
∵∠BCN=160°,
∴∠GCB=20°,
∵BG=40cm,
∴BC=$\frac{BG}{sin20°}$≈$\frac{40}{0.34}$≈118cm,
∵∠DCN=∠GCB=20°,DN=FG=7cm,
∴CD=$\frac{DN}{sin20°}$≈$\frac{7}{0.34}$≈21cm
∴钢管ABCD的长度=AB+BC+CD=25+118+21=164cm.
点评 本题考查的是解直角三角形的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若a2>a,则a>1 | B. | 若a2>a,则a2b>ab | ||
| C. | 若a2>a,则a2-b2>a-b2 | D. | 若a2>a,则-a2b<-ab |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com