
分析 (1)根据题意可得,所求方程的根与原方程的根的关系,用所求方程的根的代数式表示原方程的根,代入原方程即可得所求的方程.
(2)根据题意可得,所求方程的根与原方程的根的关系,用所求方程的根的代数式表示原方程的根,代入原方程即可得所求的方程.
解答 解:(1)设所求方程的根为y,则y=-x,所以x=-y,
把x=-y代入方程x2+x-2=0,得(-y)2+(-y)-2=0,
化简,得y2-y-2=0.
故所求方程为:y2-y-2=0.
故答案为:y2-y-2=0.
(2)设所求方程的根为y,则y=x+1,所以x=y-1,
把x=y-1代入方程x2+3x-5=0,得(y-1)2+3(y-1)-5=0,
化简,得y2+y-7=0.
故所求的方程为:y2+y-7=0.
故答案为:y2+y-7=0.
点评 本题考查阅读型问题的解答,解题的关键是明确材料中的换根法,根据实际的问题进行换根.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
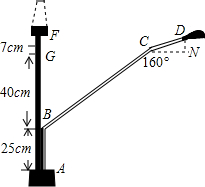 如图,马路边安装的路灯由支柱上端的钢管ABCD支撑,图中标出了相关的数据,其中CG⊥⊥AF,FD⊥AF,点G、点F分别是垂足,请根据这些信息计算钢管ABCD的长度.(钢管的直径忽略不计.结果精确到1cm.参考数据:sinθ≈0.17,cos10°≈0.98,tan10°≈0.18,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
如图,马路边安装的路灯由支柱上端的钢管ABCD支撑,图中标出了相关的数据,其中CG⊥⊥AF,FD⊥AF,点G、点F分别是垂足,请根据这些信息计算钢管ABCD的长度.(钢管的直径忽略不计.结果精确到1cm.参考数据:sinθ≈0.17,cos10°≈0.98,tan10°≈0.18,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com