
分析 (1)根据一元二次方程x2-3x+k=0有两个不相等的实数根可得△=(-3)2-4k>0,求出k的取值范围即可;
(2)根据k的取值范围,结合k为正整数,得到k的值,进而求出方程的根.
解答 解:(1)∵关于x的一元二次方程x2-3x+k=0有两个不相等的实数根,
∴△>0,即△=9-4k>0,
∴k<$\frac{9}{4}$;
(2)∵由(1)可知k<$\frac{9}{4}$,
∴选择k等于2代入原方程得:x2-3x+2=0,
解方程得:x1=2,x2=1.
点评 此题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | (x-2)2=1 | B. | (x+2)2=4 | C. | (x-2)2=-1 | D. | (x-2)2=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 录入汉字个数/人 | 132 | 133 | 134 | 135 | 136 | 137 |
| 甲班参赛学生/人 | 1 | 0 | 1 | 5 | 2 | 1 |
| 乙班参赛学生/人 | 0 | 1 | 4 | 1 | 2 | 2 |
| 平均数 | 中位数 | 众数 | 方差 | |
| 甲班 | 135 | 135 | 135 | 1.6 |
| 乙班 | 135 | 134.5 | 134 | 1.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3a+6b=9ab | B. | $\frac{1}{2}$y2-$\frac{1}{3}$y2=$\frac{1}{6}$ | C. | 8a4-6a3=2a | D. | 3a3b-3ba3=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
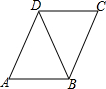 如图所示,△ABD≌△CDB,下面四个结论中,不正确的是( )
如图所示,△ABD≌△CDB,下面四个结论中,不正确的是( )| A. | △ABD和△CDB的面积相等 | B. | △ABD和△CDB的周长相等 | ||
| C. | AD∥BC,且AD=BC | D. | ∠A+∠ABD=∠C+∠CBD |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
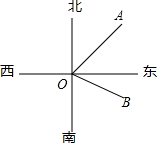 如图,在灯塔O处观测到轮船A位于东北方向,同时轮船B在南偏东55°方向,那么∠AOB的大小为( )
如图,在灯塔O处观测到轮船A位于东北方向,同时轮船B在南偏东55°方向,那么∠AOB的大小为( )| A. | 80° | B. | 90° | C. | 100° | D. | 85° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com