【题目】如图，我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形．若四边形ABCD的面积记为S1，中点四边形EFGH的面积记为S2，则S1与S2的数量关系是（ ）
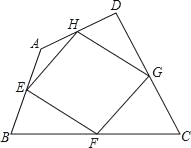
A. S1=3S2 B. 2S1=3S2 C. S1=2S2 D. 3S1=4S2
【答案】C
【解析】
根据题意由E为AB中点，且EF平行于AC，EH平行于BD，得到△BEK与△ABM相似，△AEN与△ABM相似，利用面积之比等于相似比的平方，得到△EBK面积与△ABM面积之比为1：4，且△AEN与△EBK面积相等，进而确定出四边形EKMN面积为△ABM的一半，同理得到四边形MKFP面积为△MBC面积的一半，四边形QMPG面积为△DMC面积的一半，四边形MNHQ面积为△ADM面积的一半，四个四边形面积之和即为四个三角形面积之和的一半，即为四边形ABCD面积的一半．
设AC与EH、FG分别交于点N、P，BD与EF、HG分别交于点K、Q，
∵E是AB的中点，EF∥AC，EH∥BD，
∴△EBK∽△ABM，△AEN∽△EBK，
∴
，S△AEN=S△EBK，
∴
，同理可得
，
，
，
∴
，
∴四边形ABCD的面积为S1，中点四边形EFGH的面积记为S2，则S1与S2的数量关系是S1=2S2．
故选：C．
第1卷单元月考期中期末系列答案科目：初中数学 来源： 题型：
【题目】图1是一个长为2m，宽为2m的长方形纸片，用剪刀沿图中虚线剪成四块形状大小完全一样的小长方形纸片，然后按图2的方式拼成1个空心正方形．（阴影部分为空心）
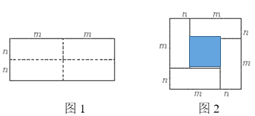
（1）请你用两种方法求图2中阴影部分的面积，直接用含m，n的代数式表示；方法① ；方法② ．
（2）观察图2，请你写出
，
三个代数式之间存在的恒等关系式；
（3）已知
，
，求的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y=ax2+bx+c（a＞0）的图象的对称轴为直线x=1，且（x1，y1），（x2，y2）为其图象上的两点，（ ）
A. 若x1＞x2＞1，则（y1-y2）+2a（x1-x2）＜0
B. 若1＞x1＞x2，则（y1-y2）+2a（x1-x2）＜0
C. 若x1＞x2＞1，则（y1-y2）+a（x1-x2）＞0
D. 若1＞x1＞x2，则（y1-y2）+a（x1-x2）＞0
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，已知抛物线y1＝x2﹣4x+4的顶点为A，直线y2＝kx﹣2k（k≠0），
（1）试说明直线是否经过抛物线顶点A；
（2）若直线y2交抛物线于点B，且△OAB面积为1时，求B点坐标；
（3）过x轴上的一点M（t，0）（0≤t≤2），作x轴的垂线，分别交y1，y2的图象于点P，Q，判断下列说法是否正确，并说明理由：
①当k＞0时，存在实数t（0≤t≤2）使得PQ＝3．
②当﹣2＜k＜﹣0.5时，不存在满足条件的t（0≤t≤2）使得PQ＝3．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】山地自行车越来越受中学生的喜爱．一网店经营的一个型号山地自行车，今年一月份销售额为30000元，二月份每辆车售价比一月份每辆车售价降价100元，若销售的数量与上一月销售的数量相同，则销售额是27000元．
（1）求二月份每辆车售价是多少元？
（2）为了促销，三月份每辆车售价比二月份每辆车售价降低了10%销售，网店仍可获利35%，求每辆山地自行车的进价是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，O为坐标原点，点A（﹣1，5）和点B（m，﹣1）均在反比例函数
图象上
（1）求m，k的值；
（2）当x满足什么条件时，﹣x+4＞﹣
；
（3）P为y轴上一点，若△ABP的面积是△ABO面积的2倍，直接写出点P的坐标．
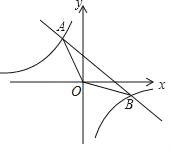
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料，并解答问题．
面积与代数恒等式
通过学习，我们知道可以用图1的面积来解释公式
，人们经常称作用面积解释代数恒等式实际上还有一些代数恒等式也可以用这种形式表示，如可用图2表示
．
请根据阅读材料，解答下列问题:
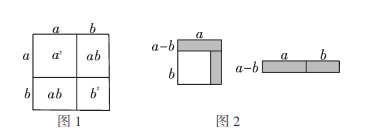
（1）请写出图3所表示的代数恒等式： ；
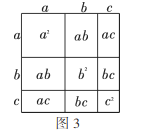
（2）试画一个几何图形，使它的面积表示：
；
（3）请仿照上述方法另写一个含有
，
的代数恒等式，并画出与它对应的几何图形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知
为等边三角形，点
为直线
上一动点(点不与点
、点
重合)．连接
，以为边向逆时针方向作等边
，连接
，
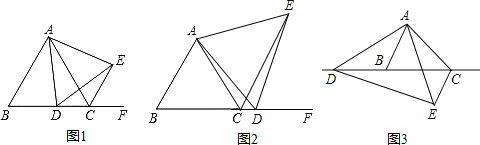
（1）如图1，当点在边上时：
①求证：
；
②判断
之间的数量关系是 ；
（2）如图2，当点在边的延长线上时，其他条件不变，判断之间存在的数量关系，并写出证明过程；
（3）如图3，当点在边的反向延长线上时，其他条件不变，请直接写出之间存在的数量关系为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
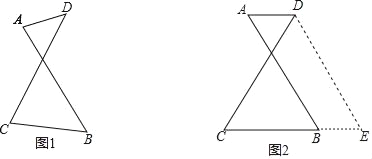
【题目】如图1有两条长度相等的相交线段AB、CD，它们相交的锐角中有一个角为60°，为了探究AD、CB与CD（或AB）之间的关系，小亮进行了如下尝试：
（1）在其他条件不变的情况下使得AD∥BC，如图2，将线段AB沿AD方向平移AD的长度，得到线段DE，然后联结BE，进而利用所学知识得到AD、CB与CD（或AB）之间的关系： ；（直接写出结果）
（2）根据小亮的经验，请对图1的情况（AD与CB不平行）进行尝试，写出AD、CB与CD（或AB）之间的关系，并进行证明；
（3）综合（1）、（2）的证明结果，请写出完整的结论： ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com