
【题目】阅读下列材料,并解答问题.
面积与代数恒等式
通过学习,我们知道可以用图1的面积来解释公式![]() ,人们经常称作用面积解释代数恒等式实际上还有一些代数恒等式也可以用这种形式表示,如可用图2表示
,人们经常称作用面积解释代数恒等式实际上还有一些代数恒等式也可以用这种形式表示,如可用图2表示![]() .
.
请根据阅读材料,解答下列问题:
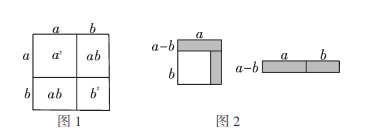
(1)请写出图3所表示的代数恒等式: ;
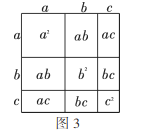
(2)试画一个几何图形,使它的面积表示:![]() ;
;
(3)请仿照上述方法另写一个含有![]() ,
,![]() 的代数恒等式,并画出与它对应的几何图形.
的代数恒等式,并画出与它对应的几何图形.
科目:初中数学 来源: 题型:
【题目】给出下面两个定理:
①线段垂直平分线上的点到这条线段两个端点的距离相等;
②到一条线段两个端点距离相等的点在这条线段的垂直平分线上.
应用上述定理进行如下推理:
如图,直线l是线段MN的垂直平分线.

∵点A在直线l上,∴AM=AN.( )
∵BM=BN,∴点B在直线l上.( )
∵CM≠CN,∴点C不在直线l上.
这是∵如果点C在直线l上,那么CM=CN, ( )
这与条件CM≠CN矛盾.
以上推理中各括号内应注明的理由依次是 ( )
A. ②①① B. ②①②
C. ①②② D. ①②①
查看答案和解析>>
科目:初中数学 来源: 题型:
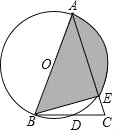
【题目】如图,在△ABC中,AB=AC,E在AC上,经过A,B,E三点的圆O交BC于点D,且D点是弧BE的中点,
(1)求证AB是圆的直径;
(2)若AB=8,∠C=60°,求阴影部分的面积;
(3)当∠A为锐角时,试说明∠A与∠CBE的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
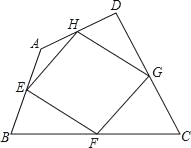
【题目】如图,我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形.若四边形ABCD的面积记为S1,中点四边形EFGH的面积记为S2,则S1与S2的数量关系是( )
A. S1=3S2 B. 2S1=3S2 C. S1=2S2 D. 3S1=4S2
查看答案和解析>>
科目:初中数学 来源: 题型:
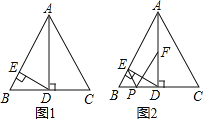
【题目】如图1,△ABC是边长为8的等边三角形,AD⊥BC下点D,DE⊥AB于点E
(1)求证:AE=3EB;
(2)若点F是AD的中点,点P是BC边上的动点,连接PE,PF,如图2所示,求PE+PF的最小值及此时BP的长;
(3)在(2)的条件下,连接EF,若AD=![]() ,当PE+PF取最小值时,△PEF的面积是 .
,当PE+PF取最小值时,△PEF的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
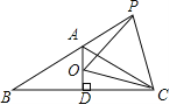
【题目】已知如图,等腰![]() 中,
中,![]() 于点
于点![]() ,点
,点![]() 是
是![]() 延长线上一点,点
延长线上一点,点![]() 是线段
是线段![]() 上一点,
上一点,![]() 下面的结论:①
下面的结论:①![]() ;②
;②![]() 是等边三角形;③
是等边三角形;③![]() ;④
;④![]() .其中正确的是( )
.其中正确的是( )
A.①②③B.①②④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个口袋里装着白、红、黑三种颜色的小球(除颜色外形状大小完全相同),其中白球3个、红球2个、黑球1个.
(1)随机从袋中取出一个球,求取出的球是黑球的概率;
(2)若取出的第一只球是红球,不将它放回袋里,从袋中余下的球中再随机地取出1个,这时取出的球是黑球的概率是多少?
(3)若取出一个球,将它放回袋中,从袋中再随机地取出一个球,两次取出的球都是白球的概率是多少?(用列表法或树状图计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,二次函数的抛物线的顶点坐标C,与x轴的交于A(1,0)、B(﹣3,0)两点,与y轴交于点D(0,3).
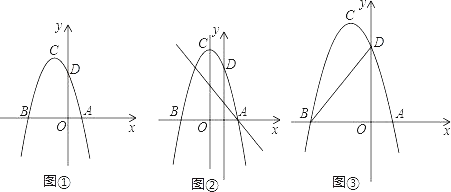
(1)求这个抛物线的解析式;
(2)如图②,过点A的直线与抛物线交于点E,交y轴于点F,其中点E的横坐标为﹣2,若直线PQ为抛物线的对称轴,点G为直线PQ上的一动点,则x轴上是否存在一点H,使D、G、H、F四点所围成的四边形周长最小?若存在,求出这个最小值及点G、H的坐标;若不存在,请说明理由;
(3)如图③,连接AC交y轴于M,在x轴上是否存在点P,使以P、C、M为顶点的三角形与△AOM相似?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,能用AAS来判定△ACD≌△ABE需要添加的条件是( )
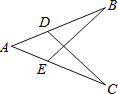
A.∠AEB=∠ADC,BE=CDB.AC=AB,∠B=∠C
C.AC=AB,AD=AED.∠AEB=∠ADC,∠B=∠C
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com