

分析 (1)由AD∥BC,得到∠G=∠ECB,根据全等三角形的判定定理即可得到结论;
(2)由△DEG≌△BCG,得到DG=BC,根据已知条件得到DG=3AD,于是得到AG=$\frac{2}{3}$BC,由△AGF∽△CBF,即可得到$\frac{AF}{BF}=\frac{AG}{BC}$=$\frac{2}{3}$.
解答 解:(1)∵AD∥BC,
∴∠G=∠ECB,
在△DEG与△BCE中,$\left\{\begin{array}{l}{∠G=∠ECB}\\{∠AEG=∠CEB}\\{DE=BE}\end{array}\right.$,
∴△DEG≌△BCG,
(2)∵△DEG≌△BCG,
∴DG=BC,
∵BC=3AD,
∴DG=3AD,
∴AG=$\frac{2}{3}$BC,
∵AD∥BC,
∴△AGF∽△CBF,
∴$\frac{AF}{BF}=\frac{AG}{BC}$=$\frac{2}{3}$.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质,平行线的性质,熟练掌握各定理是解题的关键.


科目:初中数学 来源:2017届山东省中考模拟数学试卷(解析版) 题型:解答题
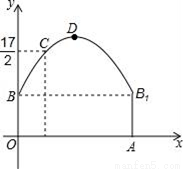
如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=﹣ x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为
x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为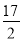 m.
m.
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (22016,0) | B. | (-21008,0) | C. | (21008,0) | D. | (0,-21008) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在Rt△ABC中,∠C=90°,D为BC边上一点且BD=2CD,连接AD并延长至E,使得AD=DE,求证:BE=$\frac{1}{2}$AE.
如图所示,在Rt△ABC中,∠C=90°,D为BC边上一点且BD=2CD,连接AD并延长至E,使得AD=DE,求证:BE=$\frac{1}{2}$AE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,等腰Rt△ABC中,∠ABC=90°,点E是点C关于点B的对称点,A(0,3),B(-1,0),则点E的坐标是(2,-1).
如图,在平面直角坐标系中,等腰Rt△ABC中,∠ABC=90°,点E是点C关于点B的对称点,A(0,3),B(-1,0),则点E的坐标是(2,-1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com