
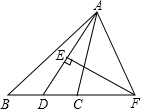
 如图,在△ABC中,∠ABC=45°,AD是∠BAC的平分线,EF垂直平分AD交BC的延长线于F,则∠CAF的度数是( )
如图,在△ABC中,∠ABC=45°,AD是∠BAC的平分线,EF垂直平分AD交BC的延长线于F,则∠CAF的度数是( )| A. | 30° | B. | 45° | C. | 75° | D. | 60° |
分析 首先根据AD是∠BAC的平分线,判断出∠BAD=∠CAD;然后根据EF垂直平分AD交BC的延长线于F,判断出∠DAF=∠ADF,进而判断出∠CAF的度数是多少即可.
解答 解:∵AD是∠BAC的平分线,
∴∠BAD=∠CAD;
∵EF垂直平分AD交BC的延长线于F,
∴∠DAF=∠ADF;
∵∠ADF=45°+∠BAD=45°+∠CAD,∠DAF=∠CAD+∠CAF
∴45°+∠CAD=∠CAD+∠CAF,
∴∠CAF=45°.
故选:B.
点评 (1)此题主要考查了线段垂直平分线的性质和应用,以及角平分线的性质和应用,要熟练掌握.
(2)此题还考查了外角的性质和应用,要熟练掌握,解答此题的关键是要明确:三角形的一个外角等于和它不相邻的两个内角的和.


科目:初中数学 来源: 题型:解答题
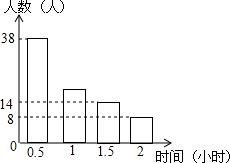 随着“微信”的流行,不少初中学生在微信朋友圈忙着“发状态”,某校在使用微信的学生中随机抽取了部分,并调查他们平常每天上微信的时间,绘制了统计表和条形统计图:
随着“微信”的流行,不少初中学生在微信朋友圈忙着“发状态”,某校在使用微信的学生中随机抽取了部分,并调查他们平常每天上微信的时间,绘制了统计表和条形统计图:| 上微信的时间(小时) | 频数(人数) | 频率 |
| 0.5 | 38 | a |
| 1 | b | 0.25 |
| 1.5 | 14 | c |
| 2 | 8 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为( )
如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为( )| A. | 5cm | B. | 10cm | C. | 20cm | D. | 5πcm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
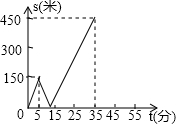 甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象的一部分如图所示.
甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象的一部分如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
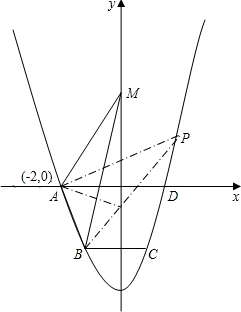 如图,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,A点到原点的距离为2,梯形的高为3,C点到y轴的距离为1,
如图,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,A点到原点的距离为2,梯形的高为3,C点到y轴的距离为1,查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不变 | B. | 扩大3倍 | C. | 缩小3倍 | D. | 扩大9倍 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com