【题目】如图，在□ABCD中，∠BAD和∠DCB的平分线AE、CF分别交BC、AD于点E、F，点M、N分别为AE、CF的中点，连接FM、EN.试判断FM和EN的数量关系和位置关系，并加以证明.

参考答案：

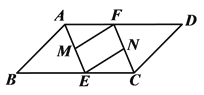
【答案】FM=EN，FM//EN.证明见解析.

【解析】试题分析：先根据已知证四边形AECF是平行四边形，再证明四边形ENFM是平行四边形即可得.

试题解析：FM=EN，FM//EN.证明如下：

∵四边形ABCD是平行四边形，∴∠BAD=∠DCB，AD∥BC，

∵AE、CF分别平分∠BAD和∠DCB，∴∠BAE=∠DAE=∠BAD，

∵AD∥BC，∴∠DAE=∠AEB，∴∠BAE=∠AEB，∴BA=BE，

同理可证DF=DC，

∵AB=CD，AD=BC，∴DF=BE，∴AF=EC，

∵AF∥EC，∴四边形AECF是平行四边形．∴AECF，

∵EM=AE，FN=CF，∴EMFN，∴四边形ENFM是平行四边形，

∴FM=EN，FM//EN.

关闭