
 如图,在正方形ABCD中,边长为2的等边△AEF的顶点E、F分别在BC和CD上,下列结论:
如图,在正方形ABCD中,边长为2的等边△AEF的顶点E、F分别在BC和CD上,下列结论:分析 根据三角形的全等的知识可以判断①的正误;根据角角之间的数量关系,以及三角形内角和为180°判断②的正误;根据线段垂直平分线的知识可以判断③的正误,根据等边三角形的边长求得直角三角形的边长,从而求得面积可以判断④的正误.
解答 解:∵四边形ABCD是正方形,
∴AB=AD,
∵△AEF是等边三角形,
∴AE=AF,
在Rt△ABE和Rt△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{AE=AF}\end{array}\right.$,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∵BC=DC,
∴BC-BE=CD-DF,
∴CE=CF,
∴①说法正确;
∵CE=CF,
∴△ECF是等腰直角三角形,
∴∠CEF=45°,
∵∠AEF=60°,
∴∠AEB=75°,
∴②说法正确;
如图,连接AC,交EF于G点,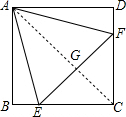
∴AC⊥EF,且AC平分EF,
∵∠CAF≠∠DAF,
∴DF≠FG,
∴BE+DF≠EF,
∴③说法错误;
∵EF=2,
∴CE=CF=$\sqrt{2}$,
∴S△EFC=$\frac{1}{2}$FC•EC=$\frac{1}{2}$×$\sqrt{2}$×$\sqrt{2}$=1
④说法正确,
∴正确的有①②④.
故答案为:①②④.
点评 本题主要考查正方形的性质的知识点,解答本题的关键是熟练掌握全等三角形的证明以及辅助线的正确作法,此题难度不大,但是有一点麻烦.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
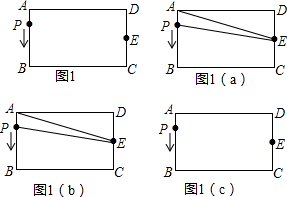
 如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2016的值为( )
如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2016的值为( )| A. | ($\frac{\sqrt{2}}{2}$)2013 | B. | ($\frac{\sqrt{2}}{2}$)2014 | C. | ($\frac{1}{2}$)2013 | D. | ($\frac{1}{2}$)2014 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点.
如图,在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
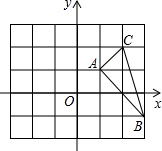 如图,在直角平面坐标系中,△ABC的顶点坐标分别是A(1,1)、B(3,-1)、C(2,2).
如图,在直角平面坐标系中,△ABC的顶点坐标分别是A(1,1)、B(3,-1)、C(2,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B、C).若线段AD长为正整数,则点D的个数共有( )
如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B、C).若线段AD长为正整数,则点D的个数共有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com