
����Ŀ����ͼ����֪������y=ax2+bx+c������A����3��0����B��9��0����C��0��4����CD��ֱ��y�ᣬ���������ڵ�D��DE��ֱ��x�ᣬ����ΪE��l�������ߵĶԳ��ᣬ��F�������ߵĶ��㣮
��1��������κ����ı���ʽ�Լ���D�����ꣻ
��2����Rt��AOC��x������ƽ�Ƶ���ֱ�DZ�OC��Գ���l�غϣ����ضԳ���l����ƽ�Ƶ���C���F�غϣ��õ�Rt��A1O1F�����ʱRt��A1O1F�����OCDE�ص����ֵ�ͼ�ε������
��3����Rt��AOC��x������ƽ��t����λ���ȣ�0��t��6���õ�Rt��A2O2C2 �� Rt��A2O2C2��Rt��OED�ص����ֵ�ͼ�������ΪS����S��t֮��ĺ�������ʽ����д���Ա���t��ȡֵ��Χ��
���𰸡�
��1��
�⣺��������y=ax2+bx+c������A����3��0����B��9��0����C��0��4����
���������ߵĽ���ʽΪy=a��x+3����x��9����
��C��0��4�����������ϣ�
��4=��27a��
��a=�� ![]() ��
��
���������ߵĽ���ʽΪy=�� ![]() ��x+3����x��9��=��
��x+3����x��9��=�� ![]() x2+
x2+ ![]() x+4��
x+4��
��CD��ֱ��y�ᣬC��0��4��
�ੁ ![]() x2+
x2+ ![]() x+4=4��
x+4=4��
��x=6��
��D��6��4����
��2��
�⣺��ͼ1��

�ߵ�F��������y=�� ![]() x2+
x2+ ![]() x+4�Ķ��㣬
x+4�Ķ��㣬
��F��3�� ![]() ����
����
��FH= ![]() ��
��
��GH��A1O1��
�� ![]() ��
��
�� ![]() ��
��
��GH=1��
��Rt��A1O1F�����OCDE�ص�����������A1O1HG��
��S�ص�����=S��A1O1F��S��FGH= ![]() A1O1��O1F��
A1O1��O1F�� ![]() GH��FH=
GH��FH= ![]() ��3��4��
��3��4�� ![]() ��1��
��1�� ![]() =
= ![]()
��3��
�ڵ�3��t��6ʱ����ͼ3��
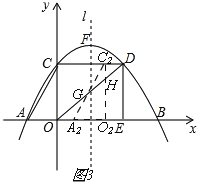
��C2H��OC��
�� ![]() ��
��
�� ![]() ��
��
��C2H= ![]() ��6��t����
��6��t����
��S=S�ı���A2O2HG=S��A2O2C2��S��C2GH
= ![]() OA��OC��
OA��OC�� ![]() C2H����t��3��
C2H����t��3��
= ![]() ��3��4��
��3��4�� ![]() ��
�� ![]() ��6��t����t��3��
��6��t����t��3��
= ![]() t2��3t+12
t2��3t+12
�൱0��t��3ʱ��S= ![]() t2����3��t��6ʱ��S=
t2����3��t��6ʱ��S= ![]() t2��3t+12
t2��3t+12
����������1���ô���ϵ�����������߽���ʽ����2����GH��A1O1 �� ���GH=1�������FH��S�ص�����=S��A1O1F��S��FGH���㼴�ɣ���3�������������ֱ���������ʽ���㣬���������������ɣ������Ƕ��κ����ۺ��⣬��Ҫ�����˴���ϵ������������ʽ��ƽ���߷��߶γɱ��������������ε�������㣬�Ȿ��Ĺؼ��ǻ���ͼ�Σ�
�����㾫����������Ŀ����֪���������������ε������ƽ���߷��߶γɱ��������֪ʶ���Եõ�����Ĵ𰸣���Ҫ���������ε����=1/2���ס��ߣ�����ƽ���߽�����ֱ�ߣ����õĶ�Ӧ�߶γɱ�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������ͬʱ�ֱ��A��B������ͬһ����·�����г���C�أ���֪A��C���ؼ�ľ���Ϊ110ǧ�ף�B��C���ؼ�ľ���Ϊ100ǧ�ף��������г���ƽ���ٶȱ��ҿ�2ǧ��/ʱ���������ͬʱ����C�أ������˵�ƽ���ٶȣ�Ϊ��������⣬���������г���ƽ���ٶ�Ϊxǧ��/ʱ���������г����̣�������ȷ���ǣ�������
A.![]() =
=![]()
B.![]() =
=![]()
C.![]() =
=![]()
D.![]() =
=![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�ž���ֽƬABCD��EF�۵���A����CD���ϵĵ�A�䴦����B���ڵ�B�䴦������2=40�㣬��ͼ�С�1�Ķ���Ϊ��������
A.115��
B.120��
C.130��
D.140��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���B=90�㣬��E��AC���е㣬AC=2AB����BAC��ƽ����AD��BC�ڵ�D����AF��BC������DE���ӳ���AF�ڵ�F������FC��
��֤���ı���ADCF�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ַ���֤���������ε���Ǻ͵���360�㡱����ͼ��
��BAE����CBF����ACD�ǡ�ABC��������ǣ�
��֤��BAE+��CBF+��ACD=360�㣮
���֤��1�������������ò�ͬ�ķ������֤��2��
��1��֤��1���� ��
���BAE+��1+��CBF+��2+��ACD+��3=180���3=540��
���BAE+��CBF+��ACD=540�㩁����1+��2+��3����
�� ��
���BAE+��CBF+��ACD=540�㩁180��=360�㣮
��2��֤��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬�Զ���AΪԲ�ģ��ʵ���Ϊ�뾶�������ֱ�AC��AB�ڵ�M��N���ٷֱ��Ե�M��NΪԲ�ģ����� ![]() MN�ij�Ϊ�뾶�������������ڵ�P��������AP����BC�ڵ�D����CD=4��AB=15�����ABD������ǣ�������
MN�ij�Ϊ�뾶�������������ڵ�P��������AP����BC�ڵ�D����CD=4��AB=15�����ABD������ǣ������� 
A.15
B.30
C.45
D.60
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�ֱ��y= ![]() x+4����x���ڵ�A����y���ڵ�C����A��C�����������F1��x������һ��B��1��0����
x+4����x���ڵ�A����y���ڵ�C����A��C�����������F1��x������һ��B��1��0���� 
��1����������F1����ʾ�Ķ��κ����ı���ʽ��
��2������M��������F1λ�ڵڶ�����ͼ���ϵ�һ�㣬���ı���MAOC�͡�BOC������ֱ�ΪS�ı���MAOC��S��BOC �� ��S=S�ı���MAOC��S��BOC �� ��S���ʱ��M�����꼰S�����ֵ��
��3����ͼ�ڣ���������F1��y�ᷭ�۲������ơ��õ�������F2 �� ��A��B�루2��������ĵ�M�Ķ�Ӧ��ֱ�ΪA�䡢B�䡢M�䣬����M����M��E��x���ڵ�E����ֱ��A��C�ڵ�D����x�����Ƿ���ڵ�P��ʹ����A�䡢D��PΪ��������������AB��C���ƣ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=x2+bx+c��ͼ���㣨4��3������3��0����
��1����b��c��ֵ��
��2������ö��κ���ͼ��Ķ�������ͶԳ��
��3������������ϵ�л������κ���y=x2+bx+c��ͼ�� 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com