
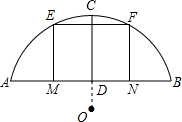
 某桥主拱桥是圆弧形,跨度AB=60m.拱高CD=10m.
某桥主拱桥是圆弧形,跨度AB=60m.拱高CD=10m.分析 (1)根据垂径定理的推论,知此圆的圆心在CD所在的直线上,设圆心是O.连接OA.根据垂径定理和勾股定理求解;
(2)连接OE,首先求得OD,假设EF=8m,由垂径定理得出EG=4m,利用勾股定理求得OG,进一步求得DG,与高度5m比较得出答案即可.
解答 解:(1)如图,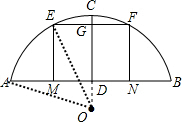
根据垂径定理的推论,知此圆的圆心在CD所在的直线上,设圆心是O
连接OA.根据垂径定理,得AD=30m,
设圆的半径是r,根据勾股定理,得r2=900+(r-10)2,
解得:r=50,
即拱桥的半径为50m.
(2)连接OE,则OD=OC-CD=40m,
假设EF=8m,则EG=4m,
OG=$\sqrt{O{E}^{2}-E{G}^{2}}$=$\sqrt{5{0}^{2}-{4}^{2}}$≈49.84m,
EM=DG=OG-OD=9.84m>5m,所以此游轮是否能顺利通过此桥.
点评 此题考查了运用了勾股定理以及垂径定理.注意构造由半径、半弦、弦心距组成的直角三角形进行有关的计算.


科目:初中数学 来源: 题型:解答题
 如图,AB∥CD,AB=CD.AD、BC相交于点O,OE=OF,BE、CF分别交AD于点E、F.根据以上信息:
如图,AB∥CD,AB=CD.AD、BC相交于点O,OE=OF,BE、CF分别交AD于点E、F.根据以上信息:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
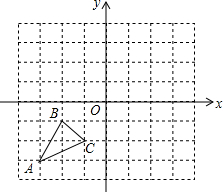 如图,已知A(-3,-3),B(-2,-1),C(-1,-2)是直角坐标平面上三点.
如图,已知A(-3,-3),B(-2,-1),C(-1,-2)是直角坐标平面上三点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
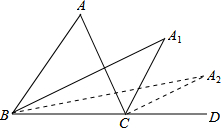 如图,在△ABC中,∠A=64°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A1BC和∠A1CD的平分线交于点A3,则∠A3=8°.
如图,在△ABC中,∠A=64°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A1BC和∠A1CD的平分线交于点A3,则∠A3=8°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
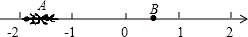 如图,一只蚂蚁从点A沿数轴向右爬行2个单位长度到达点B,点A表示-$\sqrt{2}$,设点B所表示的数为m.
如图,一只蚂蚁从点A沿数轴向右爬行2个单位长度到达点B,点A表示-$\sqrt{2}$,设点B所表示的数为m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
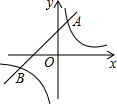 如图,函数y=$\frac{3}{x}$与函数y=x+2交于两点A(1,3),B(-3,-1),点P是y=$\frac{3}{x}$的图象上一点,当△AOP为等腰三角形时,求点P的坐标.
如图,函数y=$\frac{3}{x}$与函数y=x+2交于两点A(1,3),B(-3,-1),点P是y=$\frac{3}{x}$的图象上一点,当△AOP为等腰三角形时,求点P的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com