
����Ŀ����֪��ABC�У�AC=6cm��BC=8cm��AB=10cm�� CDΪAB���ϵĸߣ�����P�ӵ�A���������š�ABC����������ʱ����һȦ�ص�A�㣬�ٶ�Ϊ2cm/s�����˶�ʱ��Ϊts.
(1) ��CD�ij���
(2) tΪ��ֵʱ����ACPΪ���������Σ�
(3) ��MΪBC��һ���㣬NΪAB��һ���㣬�Ƿ����M��Nʹ��AM+MN��ֵ��С���������߹�����ͼ�Σ���������Сֵ�������û����˵�����ɣ�

���𰸡���1��4.8;(2) 6��8.4��9��9.5;(3)���ڣ���������������
�������������������1�����ݹ��ɶ������涨���жϡ�ABC��ֱ�������Σ����������ε������ʽ���㣻
��2���ֵ�P��BC�Ϻ�P��AB��������������ݵ��������ε��ж��������㣻
��3��������Գ�-���·����������ͼ���ɣ�
���������
��1����AC2+BC2=36+64=100��AB2=100��
��AC2+BC2=AB2��
���ABC��ֱ�������Σ�
��![]() ��AC��BC=
��AC��BC=![]() ��AB��CD��
��AB��CD��
��ã�CD=4.8cm��
��2������P��BC�ϣ�CA=CPʱ��CP=6��
��t=12��2=6s��
����P��AB�ϣ�CA=CPʱ��
��Rt��ADC��AD=![]() =3.6��
=3.6��
��ͼ��

��CA=CP��CDΪAB���ϵĸߣ�
��DP=AP=3.6��
��t=��24��7.2����2=8.4��
��AC=APʱ��t=��24��6����2=9��
��PA=PCʱ��
��ͼ����PH��AC��H��
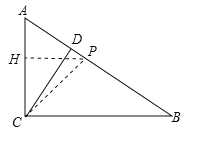
��AH=CH=3��HP=![]() BC=5��
BC=5��
�ɹ��ɶ����ã�AP=5��
��t=��24��5����2=9.5��
�ʵ�t=6��8.4��9��9.5ʱ����ACPΪ���������Σ�
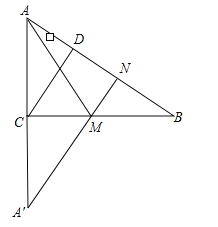
��3����ͼ����A�����BC�ĶԳƵ�A������A����AB�Ĵ���A��N������ΪN����BC��M�㣬M��N��Ϊ����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������10�֣���ͼ��ֱ��ΪAB����O��![]() ������ֱ�DZ�BC��CD�ڵ�E��F����
������ֱ�DZ�BC��CD�ڵ�E��F����![]() ������BF.
������BF.
��1����֤CDΪ��O�����ߣ���2����CF=1����D=30��ʱ����AD��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=-x2+(m-1)x+m��y�ύ�ڵ�(0��3).
��1�����m��ֵ�����������������ߣ�
��2������������x��Ľ���Ͷ������ꣻ
��3����xȡʲôֵʱ����������x���Ϸ���
��4����xȡʲôֵʱ��y��ֵ��x���������С.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и��鳤�ȵ��߶�Ϊ�ߣ��ܹ��������ε��ǣ�������
A.7cm��5cm��12cmB.4cm��6cm��5cm
C.8cm��4cm��3cmD.6cm��8cm��15cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB��AC����P��D�ֱ���BC��AC���ϵĵ㣬�ҡ�APD����B.
(1)��֤��AC��CD��CP��BP��
(2)��AB��10��BC��12����PD��ABʱ����BP�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У������ȷ���ǣ�������
A.x3x3=x6
B.3x2+2x2=5x4
C.��x2��3=x5
D.��x+y��2=x2+y2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������50�����乩�ο;�ס����ÿ�����䶨��120Ԫʱ�������ȫ��ס������ÿ������ÿ��Ķ���ÿ����10Ԫʱ���ͻ���һ��������У�����ο;�ס���䣬�������ÿ������ÿ��֧��20Ԫ�ĸ��ַ��ã���ÿ�����䶨������10xԪ��xΪ��������
��1��ֱ��д��ÿ���ο;�ס�ķ�������y��x�ĺ�����ϵʽ��
��2�������ÿ�������ΪWԪ����ÿ�䷿�۶���Ϊ����Ԫʱ������ÿ���������������������Ƕ��٣�
��3��ij�գ������˽���ס��������õ�������Ϣ���ٵ�������������5000Ԫ���ڱ���Ϊ�ο;�ס�ķ��乲֧������û�г���600Ԫ����ÿ������պ�ס��2�ˣ��ʣ����������ס���ο����������ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O���ң�OC��AB�ڵ�C������OA��AB=12����O�뾶Ϊ10��

��1����OC�ij���
��2����E��F����O�ϣ�EF��AB����EF=16��ֱ��д��EF��AB֮��ľ��룮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com