
【题目】(满分10分)如图,直径为AB的⊙O交![]() 的两条直角边BC、CD于点E、F,且
的两条直角边BC、CD于点E、F,且![]() ,连接BF.
,连接BF.
(1)求证CD为⊙O的切线;(2)当CF=1且∠D=30°时,求AD长.

【答案】(1) 证明见解析;(2) ![]() .
.
【解析】试题分析:(1)连接OF,只要证明OF∥BC,即可推出OF⊥CD,由此即可解决问题.
(2)连接AF.思想在Rt△BCF中,求出BC,再在Rt△DBC中,求出DB,在Rt△ABF中,求出AB,根据AD=DB-AB即可解决问题.
试题解析:
(1)连接OF.
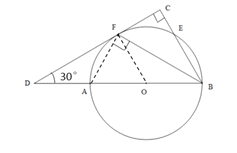
∵AF=EF ,∴∠CBF=∠FBA.
∵OF=OB,∴∠FBO=∠OFB .
∵点A、O、B三点共线,
∴∠CBF=∠OFB.
∴BC∥OF,∴∠OFC+∠C=180°.
∵∠C=90°,∴∠OFC=90°,即OF⊥DC.
∴CD为⊙O的切线.
(2) ∵∠D=30°,∴∠CBD=60°
∵AF=EF,∴∠CBF=∠DBF=![]() ∠CBD=30°
∠CBD=30°
在![]() , ∵FC=1,∠CBF=30°,∴BF=2CF=2.
, ∵FC=1,∠CBF=30°,∴BF=2CF=2.
∴![]()
连接AF.
∵AB是⊙O的直径,∴∠AFB=90°
在![]() ,∵∠ABF=30°,BF=2,∴AF=
,∵∠ABF=30°,BF=2,∴AF=![]() AB.
AB.
∴AB2=(![]() AB)2+BF2,即
AB)2+BF2,即![]() AB2=4,
AB2=4, ![]()
在![]() ,∵∠D=30°,BC=
,∵∠D=30°,BC=![]() ,∴BD=2BC=
,∴BD=2BC=![]() .
.
∴AD=DB-AB=2![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长均为1个单位长度的方格纸中,有一个[Math Processing Error] ![]()
![]() 和一点O,[Math Processing Error]
和一点O,[Math Processing Error] ![]()
![]() 的顶点与点O均与小正方形的顶点重合。
的顶点与点O均与小正方形的顶点重合。

(1)在方格纸中,将[Math Processing Error] ![]()
![]() 向下平移6个单位长度得到[Math Processing Error]
向下平移6个单位长度得到[Math Processing Error] ![]()
![]() ,请画[Math Processing Error]
,请画[Math Processing Error] ![]()
![]() .
.
(2)在方格纸中,将[Math Processing Error] ![]()
![]() 绕点O旋转180°得到[Math Processing Error]
绕点O旋转180°得到[Math Processing Error] ![]()
![]() ,请画[Math Processing Error]
,请画[Math Processing Error] ![]()
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作已知点关于某直线的对称点的第一步是( )
A.过已知点作一条直线与已知直线相交
B.过已知点作一条直线与已知直线垂直
C.过已知点作一条直线与已知直线平行
D.不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(-10,0),B(-6,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°.点P从点Q(8,0)出发,沿x轴向左以每秒1个单位长的速度向点A匀速运动,运动时间为t秒.

(1)求点C的坐标.
(2)当∠BCP=15°时,求t的值.
(3)以PC为直径作圆,当该圆与四边形ABCD的边(或边所在的直线)相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,O为坐标原点,P是反比例函数y=![]() (x>0)图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B.
(x>0)图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B.
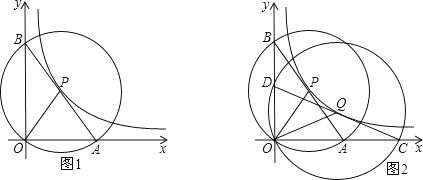
(1)求证:线段AB为⊙P的直径;
(2)求△AOB的面积;
(3)如图2,Q是反比例函数y=![]() (x>0)图象上异于点P的另一点,以Q为圆心,QO为半径画圆与坐标轴分别交于点C、D.求证:DOOC=BOOA.
(x>0)图象上异于点P的另一点,以Q为圆心,QO为半径画圆与坐标轴分别交于点C、D.求证:DOOC=BOOA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AC=6cm,BC=8cm,AB=10cm, CD为AB边上的高.动点P从点A出发,沿着△ABC的三条边逆时针走一圈回到A点,速度为2cm/s,设运动时间为ts.
(1) 求CD的长;
(2) t为何值时,△ACP为等腰三角形?
(3) 若M为BC上一动点,N为AB上一动点,是否存在M,N使得AM+MN的值最小,如果有请尺规作出图形(不必求最小值),如果没有请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com