
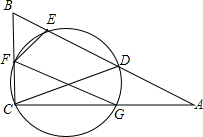
 如图,D为Rt△ABC斜边AB上一点,以CD为直径的圆分别交△ABC三边于E、F、G三点,连接FE,FG.
如图,D为Rt△ABC斜边AB上一点,以CD为直径的圆分别交△ABC三边于E、F、G三点,连接FE,FG.分析 (1)连接EC,则∠AEC=90°,由同角的余角相等即可得出∠B=∠ECA,再根据圆周角定理即可得出∠ECA=∠EFG,由此即可证出∠EFG=∠B;
(2)由AC、BC的长度利用勾股定理即可求出AB的长度,结合面积法即可得出CE的长度,由正切即可得出AE的长度,再利用勾股定理可求出CD的长度,连接FD、DG,由矩形的判定定理即可证出四边形FCGD为矩形,利用矩形的性质即可得出FG=CD,此题得解.
解答 (1)证明:连接EC,如图1所示.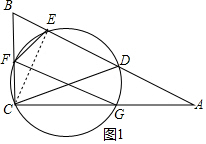
∵CD为直径,
∴∠AEC=90°,
∴∠BCE+∠B=90°.
∵∠BCE+∠ECA=90°,
∴∠B=∠ECA.
又∵∠ECA=∠EFG,
∴∠EFG=∠B;
(2)解:在Rt△BCA中,AC=4$\sqrt{5}$,BC=2$\sqrt{5}$,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10.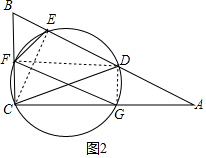
∵BC•AC=AB•CE,
∴CE=4.
∵tan∠A=$\frac{BC}{AC}$=$\frac{CE}{AE}$=$\frac{1}{2}$,
∴AE=2CE=8.
在Rt△DCG中,CE=4,ED=$\frac{1}{2}$AE=4,
∴CD=$\sqrt{C{E}^{2}+E{D}^{2}}$=4$\sqrt{2}$.
连接FD、DG,如图2所示.
∵CD是直径,
∴∠CFD=∠CGD=90°,
又∵∠FCG=90°,
∴四边形FCGD为矩形,
∴FG=CD=4$\sqrt{2}$.
点评 本题考查了圆周角定理、勾股定理、矩形的判定与性质,解题的关键是:(1)根据同角的余角相等找出∠B=∠ECA;(2)证出四边形FCGD为矩形.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙O的半径为r.A,B为⊙O上的两个不同点;以B为圆心.BA为半径的圆交⊙O于另一点C.P为⊙O内一点,使得△PAB为正三角形,CP交⊙O于另一点Q.
如图,⊙O的半径为r.A,B为⊙O上的两个不同点;以B为圆心.BA为半径的圆交⊙O于另一点C.P为⊙O内一点,使得△PAB为正三角形,CP交⊙O于另一点Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com