
【题目】某市在精准扶贫活动中,因地制宜指导农民调整种植结构,增加种植效益.2018年李大伯家在工作队的帮助下,计划种植马铃薯和蔬菜共15亩,预计每亩的投入与产出如下表:(1)如果这15亩地的纯收入要达到54900元,需种植马铃薯和蔬菜各多少亩?(2)如果总投入不超过16000元,则最多种植蔬菜多少亩?该情况下15亩地的纯收入是多少?
投入(元) | 产出(元) | |
马铃薯 | 1000 | 4500 |
蔬菜 | 1200 | 5300 |
【答案】(1)需种植马铃薯11亩,需种植蔬菜4亩;(2)最多种植蔬菜5亩,该情况下15亩地的纯收入是55500元.
【解析】
(1)设需种植马铃薯x亩,需种植蔬菜y亩,根据等量关系:一共15亩地;这15亩地的纯收入要达到54900元;列出关于x和y的二元一次方程组,解出即可;
(2)设种植马铃薯a亩,则需种植蔬菜(15﹣a)亩,根据“总投入不超过16000元”,列出关于a的一元一次不等式,解出即可.
解:(1)设需种植马铃薯x亩,需种植蔬菜y亩,依题意有
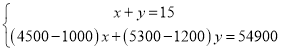 ,
,
解得![]() .
.
故需种植马铃薯11亩,需种植蔬菜4亩;
(2)设种植马铃薯a亩,则需种植蔬菜(15﹣a)亩,依题意有
1000a+1200(15﹣a)≤16000,
解得a≥10,
15﹣10=5(亩),
(4500﹣1000)×10+(5300﹣1200)×5
=35000+20500
=55500(元).
答:最多种植蔬菜5亩,该情况下15亩地的纯收入是55500元.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
【题目】在直角坐标系中,横、纵坐标都为整数的点叫做整点,设坐标轴的单位长为1cm,整点P从原点O出发,速度为1cm/秒,且点P只能向上或向右运动.请回答下列问题:
(1)填表:
从的间 | 可以得到的的坐标 | 可以得到的的个数 |
1秒 | (0,1)、(1,0) | 2 |
2秒 | (2,0)、(0,2)、 | 3 |
3秒 | (3,0)、(0,3)、 、 | 4 |
(2)当点P从点O出发10秒时,可得到的整点的个数是 个;
(3)当点P从O点出发 到整点(2,2015);
(4)当点P从点O出发30秒时,整点P横纵坐标恰好满足方程y=2x-6,请求P点坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】珠海市水务局对某小区居民生活用水情况进行了调査.随机抽取部分家庭进行统计,绘制成如下尚未完成的频数分布表和频率分布直方图.请根据图表,解答下列问题:
月均用水量(单位:吨 | 频数 | 频率 |
2≤x<3 | 4 | 0.08 |
3≤x<4 | a | b |
4≤x<5 | 14 | 0.28 |
5≤x<6 | 9 | c |
6≤x<7 | 6 | 0.12 |
7≤x<8 | 5 | 0.1 |
合计 | d | 1.00 |

(1)b= ,c= ,并补全频数分布直方图;
(2)为鼓励节约用水用水,现要确定一个用水量标准P(单位:吨),超过这个标准的部分按1.5倍的价格收费,若要使60%的家庭水费支出不受影响,则这个用水量标准P= 吨;
(3)根据该样本,请估计该小区400户家庭中月均用水量不少于5吨的家庭约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点A(-2,0).点D在y轴上,连接AD并将它沿x轴向右平移至BC的位置,且点B坐标为(4,0),连接CD,OD=![]() AB.
AB.
(1)线段CD的长为 ,点C的坐标为 ;
(2)如图2,若点M从点B出发,以1个单位长度/秒的速度沿着x轴向左运动,同时点N从原点O出发,以相同的速度沿折线OD→DC运动(当N到达点C时,两点均停止运动).假设运动时间为t秒.
①t为何值时,MN∥y轴;
②求t为何值时,S△BCM=2S△ADN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.
(1)当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;
(2)在(1)的条件下,若DE:AE:CE= 1: ![]() :3,求∠AED的度数;
:3,求∠AED的度数;
(3)若BC= 4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
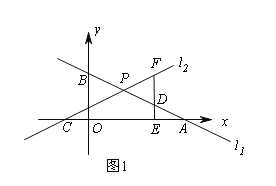
【题目】平面直角坐标系中,直线l1:![]() 与x轴交于点A,与y轴交于点B,直线l2:
与x轴交于点A,与y轴交于点B,直线l2:![]() 与x轴交于点C,与直线l1交于点P.
与x轴交于点C,与直线l1交于点P.
(1)当k=1时,求点P的坐标;
(2)如图1,点D为PA的中点,过点D作DE⊥x轴于E,交直线l2于点F,若DF=2DE,求k的值;
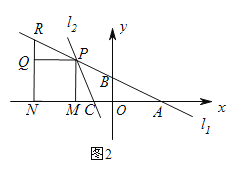
(3)如图2,点P在第二象限内,PM⊥x轴于M,以PM为边向左作正方形PMNQ,NQ的延长线交直线l1于点R,若PR=PC,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.

(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠1=∠2,G为AD的中点,BG的延长线交AC于点E,F为AB上的一点,CF与AD垂直,交AD于点H,则下面判断正确的有( )

①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;
③CH是△ACD的边AD上的高;④AH是△ACF的角平分线和高
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com