
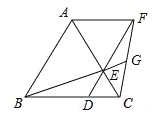
【题目】如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:
①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 .(填写所有正确结论的序号)
【答案】①②③④.
【解析】
试题分析:①由△ABC是等边三角形,可得AB=AC=BC,∠BAC=∠ACB=60°,再因DE=DC,可判定△DEC是等边三角形,所以ED=EC=DC,∠DEC=∠AEF=60°,因EF=AE,所以△AEF是等边三角形,所以AF=AE,∠EAF=60°,在△ABE和△ACF中,AB=AC,∠BAE=∠CAF,AE=AF ,可判定△ABE≌△ACF,故①正确.②由∠ABC=∠FDC,可得AB∥DF,再因∠EAF=∠ACB=60°,可得AB∥AF,即可判定四边形ABDF是平行四边形,所以DF=AB=BC,故②正确.③由△ABE≌△ACF可得BE=CF,S△ABE=S△AFC,在△BCE和△FDC中,BC=DF,CE=CD,BE=CF ,可判定△BCE≌△FDC,所以S△BCE=S△FDC,即可得S△ABC=S△ABE+S△BCE=S△ACF+S△BCE=S△ABC=S△ACF+S△DCF,故③正确.④由△BCE≌△FDC,可得∠DBE=∠EFG,再由∠BED=∠FEG可判定△BDE∽△FGE,所以![]() ,即
,即![]() ,又因BD=2DC,DC=DE,可得
,又因BD=2DC,DC=DE,可得![]() =2,即FG=2EG.故④正确.
=2,即FG=2EG.故④正确.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】袋子中装有2个黑球和3个白球,这些球除了颜色不同外形状、大小、质地等完全相同,在看不到球的条件下,随机地一次从袋子中摸出三个球.下列事件是必然事件的是( )
A.摸出的三个球中至少有一个球是白球
B.摸出的三个球中至少有一个球是黑球
C.摸出是三个球中至少有两个球的黑球
D.摸出的单个球中至少有两个球是白球
查看答案和解析>>
科目:初中数学 来源: 题型:
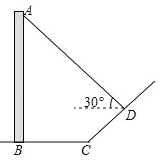
【题目】(2016山东潍坊第22题)如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形的三边长a,b,c满足2ab=(a+b)2﹣c2,则此三角形是( )
A. 钝角三角形 B. 锐角三角形 C. 直角三角形 D. 等边三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
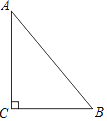
【题目】如图是一块直角三角形的绿地,量得直角边BC为6cm,AC为8cm,现在要将原绿地扩充后成等腰三角形,且扩充的部分是以AC为直角边的直角三角形,求扩充后的等腰三角形绿地的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com