
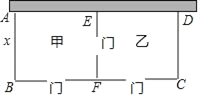
【题目】林场要建一个果园(矩形ABCD),果园的一面靠墙(墙最大可用长度为30米),另三边用木栏围成,中间EF也用木栏隔开,分为甲、乙两个场地,并在如图所示的三处各留1米宽的门(不用木栏),木栏总长57米.设果园(矩形ABCD)的宽AB为x米,矩形ABCD的面积为S平方米.
(1)求S关于x的函数表达式,并写出自变量x的取值范围.
(2)求果园能达到的最大面积S及相应x的值.
(3)若木栏BF比CF多10米,其余条件不变,甲场地种植葡萄,一季平均每平方米收益40元;乙场地种植益莓,一季平均每平方米收益160元.问该果园一季能达到的最大收益W为多少元?
【答案】(1)S=﹣3x2+60x ,10≤x<20(2)300m2(3)24000元
【解析】
(1)由AB=x得出BC=60﹣3x,再根据矩形的面积公式可得函数解析式;
(2)将(1)中所得函数解析式配方成顶点式,利用二次函数的性质解答即可;
(3)由BC=60﹣3x且木栏BF比CF多10米得出BF=![]() +5=35﹣1.5x,CF=
+5=35﹣1.5x,CF=![]() ﹣5=25﹣1.5x,根据“总收益=葡萄总收益+益莓总收益”列出函数解析式,继而利用二次函数的性质求解可得.
﹣5=25﹣1.5x,根据“总收益=葡萄总收益+益莓总收益”列出函数解析式,继而利用二次函数的性质求解可得.
(1)由题意可知,∵AB=x,
∴BC=60﹣3x.
∴S=x(60﹣3x)=﹣3x2+60x.
由BC=60﹣3x≤30,且60﹣3x>0,
可得自变量x的取值范围是:10≤x<20.
(2)因为S=﹣3x2+60x=﹣3(x﹣10)2+300,
所以x=﹣![]() =10m时,S最大值=300m2.
=10m时,S最大值=300m2.
(3)∵BC=60﹣3x,即BF+CF=60﹣3x,
∴BF=![]() +5=35﹣1.5x,CF=
+5=35﹣1.5x,CF=![]() ﹣5=25﹣1.5x.
﹣5=25﹣1.5x.
∴W=40x(35﹣1.5x)+160x(25﹣1.5x)
=﹣300x2+5400x (10≤x<![]() ),
),
x=﹣![]() =9,但不在取值范围内,
=9,但不在取值范围内,
由函数增减性可知,当x=10m时,W最大=24000元.
答:该果园一季能达到的最大收益W为24000元.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与x轴交于A.B两点,与y轴交于C点,抛物线的顶点为D点,点A的坐标为(﹣1,0).
与x轴交于A.B两点,与y轴交于C点,抛物线的顶点为D点,点A的坐标为(﹣1,0).
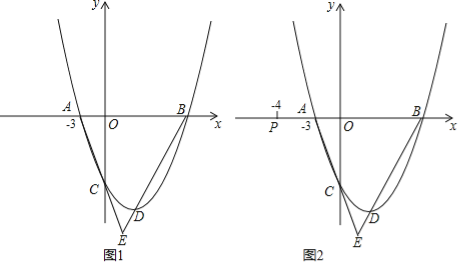
(1)求D点的坐标;
(2)如图1,连接AC,BD并延长交于点E,求∠E的度数;
(3)如图2,已知点P(﹣4,0),点Q在x轴下方的抛物线上,直线PQ交线段AC于点M,当∠PMA=∠E时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列一段文字,然后回答下列问题.
已知平面内两点 M(x1,y1)、N(x2,y2),则这两点间的距离可用下列公式计算: MN= ![]() .
.
例如:已知 P(3,1)、Q(1,﹣2),则这两点间的距离 PQ=![]() =
=![]() .
.
特别地,如果两点 M(x1,y1)、N(x2,y2)所在的直线与坐标轴重合或平行于坐标轴或垂直于坐 标轴,那么这两点间的距离公式可简化为 MN=丨 x1﹣x2 丨或丨 y1﹣y2 丨.
(1)已知 A(1,2)、B(﹣2,﹣3),试求 A、B 两点间的距离;
(2)已知 A、B 在平行于 x 轴的同一条直线上,点 A 的横坐标为 5,点 B 的横坐标为﹣1,
试求 A、B 两 点间的距离;
(3)已知△ABC 的顶点坐标分别为 A(0,4)、B(﹣1,2)、C(4,2),你能判定△ABC 的形状 吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知像这样由7个全等的正六边形组成的图形叫做“二环蜂窝”,每个正六边形的顶点叫做格点,顶点都在格点上的三角形叫做格点三角形.已知△ABC为该二环蜂窝一个格点三角形,则在该二环蜂窝中,以点A为顶点且与△ABC相似(包括全等但不与△ABC重合)的格点三角形最多能作的个数为( )
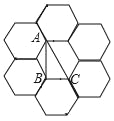
A. 18 B. 23 C. 25 D. 28
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.
恒成立的结论有 .(把你认为正确的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
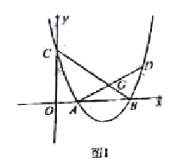
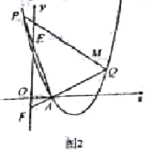
【题目】抛物线 y=x2+mx+n 过点(-1,8)和点(4,3)且与 x 轴交于 A,B 两点, 与 y 轴交于点 C
(1)求抛物线的解析式;
(2)如图1,AD 交抛物线于 D,交直线 BC 于点 G,且 AG=GD,求点 D 的坐标;
(3)如图2,过点 M(3,2)的直线交抛物线于 P,Q,AP 交 y 轴于点 E,AQ 交y 轴于点 F,求OE·OF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
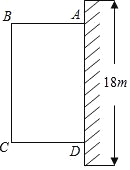
【题目】为了改善小区环境,某小区决定要在一块边靠墙(墙长18m)的空地,修建一个矩形绿地ABCD,绿地一边靠墙,另三边用总长为40m的栅栏围住(如图),设AB边为xm,绿地面积为ym2.
(1)求y与x之间的函数关系,并求出自变量x的取值范围;
(2)绿地的面积能不能为200m2?如果能,求出x的值,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
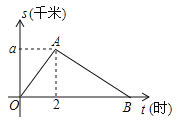
【题目】某单位举行“健康人生”徒步走活动,某人从起点体育村沿建设路到市生态园,再沿原路返回,设此人离开起点的路程s(千米)与徒步时间t(小时)之间的函数关系如图所示,其中从起点到市生态园的平均速度是4千米/小时,用2小时,根据图象提供信息,解答下列问题.
(1)求图中的a值.
(2)若在距离起点5千米处有一个地点C,此人从第一次经过点C到第二次经过点C,所用时间为1.75小时.
①求AB所在直线的函数解析式;
②请你直接回答,此人走完全程所用的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com