
【题目】如图,点![]() 在以
在以![]() 为直径的
为直径的![]() 上,点
上,点![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 垂直于
垂直于![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
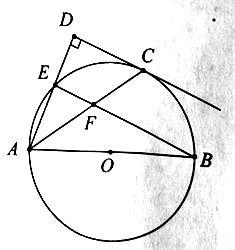
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)16.
【解析】
试题分析:(1)连接OC,由点C是![]() 的中点利用垂径定理可得出OC⊥BE,由AB是⊙O的直径可得出AD⊥BE,进而可得出AD∥OC,再根据AD⊥CD可得出OC⊥CD,由此即可证出CD是⊙O的切线.
的中点利用垂径定理可得出OC⊥BE,由AB是⊙O的直径可得出AD⊥BE,进而可得出AD∥OC,再根据AD⊥CD可得出OC⊥CD,由此即可证出CD是⊙O的切线.
(2)过点O作OM⊥AC于点M,由点C是![]() 的中点利用圆周角定理可得出∠BAC=∠CAE,根据角平分线的定理结合cos∠CAD=
的中点利用圆周角定理可得出∠BAC=∠CAE,根据角平分线的定理结合cos∠CAD=![]() 可求出AB的长度,在Rt△AOM中,通过解直角三角形可求出AM的长度,再根据垂径定理即可得出AC的长度.
可求出AB的长度,在Rt△AOM中,通过解直角三角形可求出AM的长度,再根据垂径定理即可得出AC的长度.
试题解析:(1)证明:连接OC,如图1所示.
∵点C是![]() 的中点,∴
的中点,∴![]() ,∴OC⊥BE.
,∴OC⊥BE.
∵AB是⊙O的直径,∴AD⊥BE,∴AD∥OC.
∵AD⊥CD,∴OC⊥CD,
∴CD是⊙O的切线.
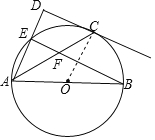
(2)解:过点O作OM⊥AC于点M,如图2所示.
∵点C是![]() 的中点,∴
的中点,∴![]() ,∠BAC=∠CAE,
,∠BAC=∠CAE,
∴![]() .
.
∵cos∠CAD=![]() ,∴
,∴![]() ,∴AB=
,∴AB=![]() BF=20.
BF=20.
在Rt△AOM中,∠AMO=90°,AO=![]() AB=10,cos∠OAM=cos∠CAD=
AB=10,cos∠OAM=cos∠CAD=![]() ,
,
∴AM=AOcos∠OAM=8,∴AC=2AM=16.


科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.如果 ![]() =1,那么a=1;
=1,那么a=1;
B.三个内角分别对应相等的两个三角形全等;
C.如果a是有理数,那么a是实数 ;
D.两边一角对应相等的两个三角形全等。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠1=18°18′,∠2=18.18°,∠3=18.3°,下列结论正确的是( )
A. ∠1=∠3B. ∠1=∠2C. ∠2=∠3D. ∠1=∠2=∠3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△ADE都是等边三角形.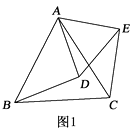
(1)求证:BD=CE;
(2)如图2,若BD的中点为P , CE的中点为Q , 请判断△APQ的形状,并说明理由.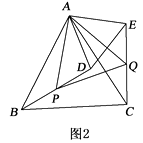
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:
甲 | 8 | 9 | 7 | 9 | 8 | 6 | 7 | 8 | 10 | 8 |
乙 | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
且 ![]() =8,S乙2=1.8,S甲2=1.2,根据上述信息完成下列问题:
=8,S乙2=1.8,S甲2=1.2,根据上述信息完成下列问题:
(1)乙运动员射击训练成绩的众数是 , 中位数是 .
(2)求甲运动员射击成绩的平均数,并判断甲、乙两人在本次射击成绩的稳定性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某广告公司设计一幅周长为16米的矩形广告牌,广告设计费为每平方米2000元.设矩形一边长为x,面积为S平方米.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围;
(2)设计费能达到24000元吗?为什么?
(3)当x是多少米时,设计费最多?最多是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com