
【题目】如图,∠AOB=120°,OP平分∠AOB,且OP=3,若点M,N分别在OA,OB上,ΔPMN为等边三角形,则满足上述条件的△PMN有中( )

A.1个B.2个C.3个D.3个以上
【答案】D
【解析】
首先在OA、OB上截取OE=OF=OP,作∠MPN=60°,由OP平分∠AOB,∠EOP=∠POF=60°,OP=OE=OF,判断出△OPE,△OPF是等边三角形,得出EP=OP,∠EPO=∠OEP=∠PON=∠MPN=60°,进而得出∠EPM=∠OPN,再由ASA判定△PEM≌△PON,得出PM=PN,又∠MPN=60°,可知△PNM是等边三角形,因此只要∠MPN=60°,△PMN就是等边三角形,故这样的三角形有无数个.
解:如图在OA、OB上截取OE=OF=OP,作∠MPN=60°

∵OP平分∠AOB,
∴∠EOP=∠POF=60°,
∵OP=OE=OF,
∴△OPE,△OPF是等边三角形,
∴EP=OP,∠EPO=∠OEP=∠PON=∠MPN=60°,
∴∠EPM=∠OPN,
在△PEM和△PON中,
∴△PEM≌△PON(ASA).
∴PM=PN,
∵∠MPN=60°,
∴△PNM是等边三角形,
∴只要∠MPN=60°,△PMN就是等边三角形,
故这样的三角形有无数个,
故选D


科目:初中数学 来源: 题型:
【题目】如图,在△ABE中,∠BAE=105°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )

A. 45°B. 60°C. 50°D. 55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为使中华传统文化教育更具有实效性,军宁中学开展以“我最喜爱的传统文化种类”为主题的调查活动,围绕“在诗词、国画、对联、书法、戏曲五种传统文化中,你最喜爱哪一种?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题:
(1)本次调查共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)若军宁中学共有960名学生,请你估计该中学最喜爱国画的学生有多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC的边AB,AC的外侧分别作等边△ABD和等边△ACE,连接DC,BE.
(1)求证:DC=BE;
(2)若BD=3,BC=4, BD⊥BC于点B,请求出△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点![]() 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为
周长的最小值为![]()
![]()

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
如图①,在△ABC的边AB上取一点P,连接CP,可以把△ABC分成两个三角形,如果这两个三角形都是等腰三角形,我们就称点P是△ABC的边AB上的和谐点.

解决问题:
(1)如图②,在△ABC中,∠ACB=90°,试找出边AB上的和谐点P,并说明理由:
(2)己知∠A=36°,△ABC的顶点B在射线l上(如图③),点P是边AB上的和谐点,请在图③及备用图中画出所有符合条件的点B,用同一标记标上相等的边,并写出相应的∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)(1)阅读理解:
如图1,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD,把AB,AC,2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是_________;
(2)问题解决:
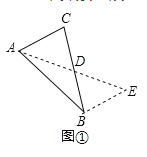

如图2,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证BE+CF>EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在实验中我们常常采用利用计算机在平面直角坐标系中画出抛物线![]() 和直线
和直线![]() ,利用两图象交点的横坐标来求一元二次方程
,利用两图象交点的横坐标来求一元二次方程![]() 的解,也可以在平面直角坐标系中画出抛物线
的解,也可以在平面直角坐标系中画出抛物线![]() 和直线
和直线![]() ,用它们交点的横坐标来求该方程的解.所以求方程
,用它们交点的横坐标来求该方程的解.所以求方程![]() 的近似解也可以利用熟悉的函数________和________的图象交点的横坐标来求得.
的近似解也可以利用熟悉的函数________和________的图象交点的横坐标来求得.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+x+3的顶点为P,与y轴交于点A,若向右平移4个单位,向下平移4个单位,则抛物线上PA段扫过的区域(阴影部分)的面积为__________.
x2+x+3的顶点为P,与y轴交于点A,若向右平移4个单位,向下平移4个单位,则抛物线上PA段扫过的区域(阴影部分)的面积为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com