Question

【题目】（题文）(1)阅读理解：

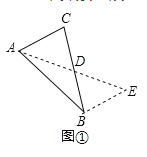
如图1，在△ABC中，若AB＝10，AC＝6，求BC边上的中线AD的取值范围．

解决此问题可以用如下方法：延长AD到点E使DE＝AD，连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD，把AB，AC，2AD集中在△ABE中．利用三角形三边的关系即可判断中线AD的取值范围是_________；

(2)问题解决：

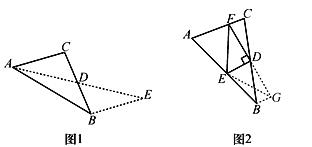
如图2，在△ABC中，D是BC边上的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，求证BE＋CF＞EF.

Answer 1

【答案】（1）2<AD<8（2）证明见解析

【解析】试题分析：（1）延长AD到E，使AD=DE，连接BE，△ADC≌△EDB，推出EB=AC，根据三角形的三边关系求出即可；
（2）先利用ASA判定△BGD≌△CFD，从而得出BG=CF；再利用全等的性质可得GD=FD，BG=CF，再有DE⊥DF，从而得出EG=EF，两边和大于第三边从而得出BE+CF>EF.

试题解析：(1)延长AD到E，使AD=DE，连接BE，

∵AD是△ABC的中线，

∴BD=CD，

在△ADC与△EDB中,

∴△ADC≌△EDB(SAS)，

∴EB=AC，

根据三角形的三边关系得：ABAC<AE<AC+AB，

∴4<AE<16，

∵AE=2AD

∴2<AD<8，

即：BC边上的中线AD的取值范围2<AD<8；

故答案为：2<AD<8.

(2)BE+CF>EF.

理由：如图2，

过点B作交FD的延长线于G，

∴∠DBG=∠DCF.

∵D为BC的中点，

∴BD=CD

又∵∠BDG=∠CDF，

在△BGD与△CFD中,

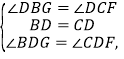
∴△BGD≌△CFD(ASA).

∴GD=FD，BG=CF.

又∵DE⊥DF，

∴EG=EF(垂直平分线到线段端点的距离相等).

∴在△EBG中，BE+BG>EG，

即BE+CF>EF.