练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在Rt△ABC中，∠ACB=90°，AC=BC=1，将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE，点B经过的路径为 ，则图中阴影部分的面积是 ．

    【答案】
    【解析】解：∵∠ACB=90°，AC=BC=1， ∴AB= ，
    ∴S扇形ABD= = ．
    又∴Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE，
    ∴Rt△ADE≌Rt△ACB，
    ∴S阴影部分=S△ADE+S扇形ABD﹣S△ABC=S扇形ABD= ．
    故答案为： ．
    先根据勾股定理得到AB= ，再根据扇形的面积公式计算出S扇形ABD ， 由旋转的性质得到Rt△ADE≌Rt△ACB，于是S阴影部分=S△ADE+S扇形ABD﹣S△ABC=S扇形ABD

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

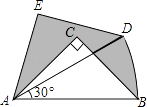
    科目：初中数学 来源： 题型：

    【题目】对于不等式组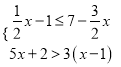 下列说法正确的是（　　）

    A. 此不等式组无解 B. 此不等式组有7个整数解

    C. 此不等式组的负整数解是﹣3，﹣2，﹣1 D. 此不等式组的解集是＜x≤2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

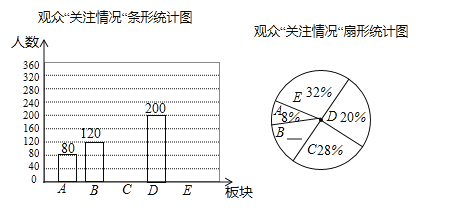
    【题目】“2016国际大数据产业博览会”于5月25日至5月29日在贵阳举行．参展内容为：A﹣经济和社会发展；B﹣产业与应用；C﹣技术与趋势；D﹣安全和隐私保护；E﹣电子商务，共五大板块，为了解观众对五大板块的“关注情况”，某机构进行了随机问卷调查，并将调查结果绘制成如下两幅统计图（均不完整），请根据统计图中提供的信息，解答下列问题：

    （1）本次随机调查了多少名观众？

    （2）请补全统计图，并求出扇形统计图中“D﹣安全和隐私保护”所对应的扇形圆心角的度数．

    （3）据相关报道，本次博览会共吸引力90000名观众前来参观，请估计关注“E﹣电子商务”的人数是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y=x2﹣2x+m﹣1与x轴只有一个交点，且与y轴交于A点，如图，设它的顶点为B．

    （1）求m的值；
    （2）过A作x轴的平行线，交抛物线于点C，求证：△ABC是等腰直角三角形；

    （3）将此抛物线向下平移4个单位后，得到抛物线C′，且与x轴的左半轴交于E点，与y轴交于F点，如图．请在抛物线C′上求点P，使得△EFP是以EF为直角边的直角三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果一元一次方程的根是一元一次不等式组的解，则称该一元一次方程为该不等式组的伴随方程，这个根在数轴上对应的点该不等式组的伴随点．

    （1）在方程①，②，③中，不等式组 的伴随方程是 ；（填序号）

    （2）如图，M、N都是关于的不等式组的伴随点，求的取值范围．

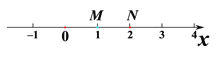
    （3）不等式组的伴随方程的根有且只有2个整数，求的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（题文）(1)阅读理解：

    如图1，在△ABC中，若AB＝10，AC＝6，求BC边上的中线AD的取值范围．

    解决此问题可以用如下方法：延长AD到点E使DE＝AD，连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD，把AB，AC，2AD集中在△ABE中．利用三角形三边的关系即可判断中线AD的取值范围是_________；

    (2)问题解决：

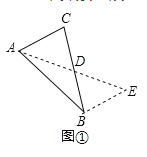
    如图2，在△ABC中，D是BC边上的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，求证BE＋CF＞EF.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点P(x，y)在第二象限，则点P的坐标可能是_____（写出一个即可）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在三角形纸片ABC中，已知∠ABC=90°，AB=6，BC=8．过点A作直线l平行于BC，折叠三角形纸片ABC，使直角顶点B落在直线l上的T处，折痕为MN．当点T在直线l上移动时，折痕的端点M、N也随之移动．若限定端点M、N分别在AB、BC边上移动，则线段AT长度的最大值与最小值之和为（计算结果不取近似值）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列语句中正确的是（ ）

    A.两个三角形的面积相等，那么这两个三角形全等

    B.三个内角对应相等的两个三角形全等

    C.两个等腰直角三角形全等，那么它们的斜边相等

    D.两边及其中一边所对的角对应相等的两个三角形全等

    查看答案和解析>>

    同步练习册答案