
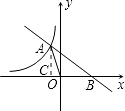
【题目】右图中曲线是反比例函数 ![]() 的图象的一支.
的图象的一支.
(1)这个反比例函数图象的另一支位于哪个象限?常数n的取值范围是什么?
(2)若一次函数 ![]() 的图象与反比例函数的图象交于点A,与x轴交于点B,△AOB的面积为2,求n的值.
的图象与反比例函数的图象交于点A,与x轴交于点B,△AOB的面积为2,求n的值.
【答案】
(1)
解:这个反比例函数图象的另一支位于第四象限.
由n+7<0,
解得n<﹣7,
即常数n的取值范围是n<﹣7
(2)
解:在 ![]() 中令y=0,得x=2,
中令y=0,得x=2,
即OB=2.
过A作x轴的垂线,垂足为C,如图.
∵S△AOB=2,即 ![]() OBAC=2,
OBAC=2,
∴ ![]() ×2×AC=2,解得AC=2,即A点的纵坐标为2.
×2×AC=2,解得AC=2,即A点的纵坐标为2.
把y=2代入 ![]() 中,得x=﹣1,即A(﹣1,2).
中,得x=﹣1,即A(﹣1,2).
所以 ![]() ,
,
解得n=﹣9
【解析】(1)根据反比例函数的性质可求得反比例函数的图象分布在第二、第四象限,所以n+7<0即可求解;(2)图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S= ![]() |k|,可利用△AOB的面积求出n值.
|k|,可利用△AOB的面积求出n值.
【考点精析】关于本题考查的反比例函数的图象和反比例函数的性质,需要了解反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点;性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大才能得出正确答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列各式,属于二元一次方程的个数有( )
①xy+2x-y=7; ②4x+1=x-y; ③![]() +y=5; ④x=y; ⑤x2-y2=2
+y=5; ④x=y; ⑤x2-y2=2
⑥6x-2y ⑦x+y+z=1 ⑧y(y-1)=2y2-y2+x
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鲁班家装公司为芙蓉小区做家装设计,调查员设计了如下问卷,对家装风格进行专项调查. 
通过随机抽样调查50家客户,得到如下数据:
A B B A B B A C A C A B A D A A B
B A A D B A B A C A C B A A D A A
A B B D A A A B A C A B D A B A
(1)请你补全下面的数据统计表: 家装风格统计表
装修风格 | 划记 | 户数 | 百分比 |
A中式 | 正正正正正 | 25 | 50% |
B欧式 | |||
C韩式 | 5 | 10% | |
D其他 | 正 | 10% | |
合计 | 50 | 100% |
(2)请用扇形统计图描述(1)表中的统计数据;(注:请标明各部分的圆心角度数)
(3)如果公司准备招聘10名装修设计师,你认为各种装修风格的设计师应分别招多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
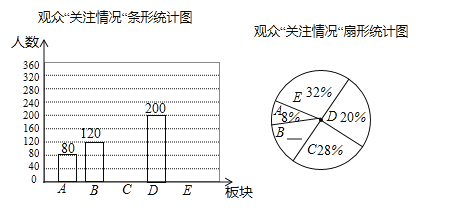
【题目】“2016国际大数据产业博览会”于5月25日至5月29日在贵阳举行.参展内容为:A﹣经济和社会发展;B﹣产业与应用;C﹣技术与趋势;D﹣安全和隐私保护;E﹣电子商务,共五大板块,为了解观众对五大板块的“关注情况”,某机构进行了随机问卷调查,并将调查结果绘制成如下两幅统计图(均不完整),请根据统计图中提供的信息,解答下列问题:
(1)本次随机调查了多少名观众?
(2)请补全统计图,并求出扇形统计图中“D﹣安全和隐私保护”所对应的扇形圆心角的度数.
(3)据相关报道,本次博览会共吸引力90000名观众前来参观,请估计关注“E﹣电子商务”的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王伟准备用一段长30米的篱笆围成一个三角形形状的小圈,用于饲养家兔.已知第一条边长为a米,由于受地势限制,第二条边长只能是第一条边长的2倍多2米.
(1)请用a表示第三条边长;
(2)问第一条边长可以为7米吗?请说明理由,并求出a的取值范围;
(3)能否使得围成的小圈是直角三角形形状,且各边长均为整数?若能,说明你的围法;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣2x+m﹣1与x轴只有一个交点,且与y轴交于A点,如图,设它的顶点为B.
(1)求m的值;
(2)过A作x轴的平行线,交抛物线于点C,求证:△ABC是等腰直角三角形;
(3)将此抛物线向下平移4个单位后,得到抛物线C′,且与x轴的左半轴交于E点,与y轴交于F点,如图.请在抛物线C′上求点P,使得△EFP是以EF为直角边的直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)(1)阅读理解:
如图1,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD,把AB,AC,2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是_________;
(2)问题解决:
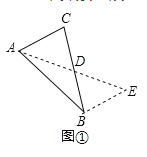

如图2,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证BE+CF>EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从分别标有数﹣3,﹣2,﹣1,0,1,2,3的七张没有明显差别的卡片中,随机抽取一张,所抽卡片上的数的绝对值不是正数的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com