
【题目】如图,在△ABC中,∠ACB=90°,点D,E在AB上,且AF垂直平分CD,BG垂直平分CE.(1)求∠ECD的度数;(2)若∠ACB为α,则∠ECD的度数能否用含α的式子来表示.

【答案】见解析
【解析】试题分析:
(1)由AF垂直平分CD可得AC=AD,再由等腰三角形的“三线合一”可得∠FAB=![]() ∠CAB,同理可得∠GBA=
∠CAB,同理可得∠GBA=![]() ∠CBA;如图,设AF、BG相交于点O,则∠GOF=∠AOB=180°-∠FAB-∠GBA=180°-
∠CBA;如图,设AF、BG相交于点O,则∠GOF=∠AOB=180°-∠FAB-∠GBA=180°-![]() (180°-∠ACB)=135°,由此在四边形GOFC中可得∠ECD=360°-∠CGO-∠CFO-∠GOF=360°-90°-90°-∠GOF=180°-135°=45°.
(180°-∠ACB)=135°,由此在四边形GOFC中可得∠ECD=360°-∠CGO-∠CFO-∠GOF=360°-90°-90°-∠GOF=180°-135°=45°.
(2)思路同(1)只需把∠ACB=90°换成∠ACB= ![]() 可解得∠DCE=90°-
可解得∠DCE=90°- ![]() .
.
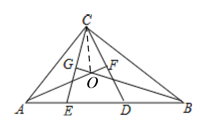
试题解析:
(1)如图,设AF、BG相交于点O,连接CO,
∵AF垂直平分CD,
∴AC=AD,∠CFO=90°,∴∠FAB=![]() ∠CAB.
∠CAB.
同理可得:∠CGO=90°,∠GBA=![]() ∠CBA.
∠CBA.
∴∠GOF=∠AOB=180°-∠FAB-∠GBA=180°-![]() (180°-∠ACB)=90°+
(180°-∠ACB)=90°+![]() ∠ACB=135°,
∠ACB=135°,
∵四边形GOFC的内角和为360°,
∴∠ECD=360°-∠CGO-∠CFO-∠GOF
=360°-90°-90°-∠GOF
=180°-135°
=45°.
(2)同(1)可得∠GOF=90°+![]() ∠ACB=90°+
∠ACB=90°+ ![]() ,∠CFO=90°,∠CGO=90°,
,∠CFO=90°,∠CGO=90°,
∵四边形GOFC的内角和为360°,
∴∠ECD=360°-∠CGO-∠CFO-∠GOF
=360°-90°-90°-∠GOF
=180°-(90°+ ![]() )
)
=90°- ![]() .
.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:
【题目】某高校共有5个大餐厅和2个小餐厅。经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐。
(1)1个大餐厅和1个小餐厅分别可供多少名学生就餐?
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,正方形A1B1C1O1、A2B2C2C1、…、AnBnCnCn﹣1按如图所示的方式放置,其中点A1、A2、A3、…、An均在一次函数y=kx+b的图象上,点C1、C2、C3、…、Cn均在x轴上.若点B1的坐标为(1,1),点B2的坐标为(3,2),则点An的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于不等式组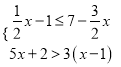 下列说法正确的是( )
下列说法正确的是( )
A. 此不等式组无解 B. 此不等式组有7个整数解
C. 此不等式组的负整数解是﹣3,﹣2,﹣1 D. 此不等式组的解集是![]() <x≤2
<x≤2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式,属于二元一次方程的个数有( )
①xy+2x-y=7; ②4x+1=x-y; ③![]() +y=5; ④x=y; ⑤x2-y2=2
+y=5; ④x=y; ⑤x2-y2=2
⑥6x-2y ⑦x+y+z=1 ⑧y(y-1)=2y2-y2+x
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鲁班家装公司为芙蓉小区做家装设计,调查员设计了如下问卷,对家装风格进行专项调查. 
通过随机抽样调查50家客户,得到如下数据:
A B B A B B A C A C A B A D A A B
B A A D B A B A C A C B A A D A A
A B B D A A A B A C A B D A B A
(1)请你补全下面的数据统计表: 家装风格统计表
装修风格 | 划记 | 户数 | 百分比 |
A中式 | 正正正正正 | 25 | 50% |
B欧式 | |||
C韩式 | 5 | 10% | |
D其他 | 正 | 10% | |
合计 | 50 | 100% |
(2)请用扇形统计图描述(1)表中的统计数据;(注:请标明各部分的圆心角度数)
(3)如果公司准备招聘10名装修设计师,你认为各种装修风格的设计师应分别招多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)(1)阅读理解:
如图1,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD,把AB,AC,2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是_________;
(2)问题解决:
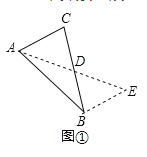

如图2,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证BE+CF>EF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com