
【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件![]() 元,出厂价为每件
元,出厂价为每件![]() 元,每月销售量
元,每月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的关系近似满足一次函数:
(元)之间的关系近似满足一次函数:![]() .
.
(1)李明在开始创业的第一个月将销售单价定为![]() 元,那么政府这个月为他承担的总差价为多少元?
元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为![]() (元),当销售单价定为多少元时,每月可获得最大利润?
(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于![]() 元.如果李明想要每月获得的利润不低于
元.如果李明想要每月获得的利润不低于![]() 元,那么政府为他承担的总差价最少为多少元?
元,那么政府为他承担的总差价最少为多少元?
【答案】(1)政府这个月为他承担的总差价为600元;
(2)当销售单价定为30元时,每月可获得最大利润4000元;
(3)销售单价定为25元时,政府每个月为他承担的总差价最少为500元.
【解析】
试题(1)把x=20代入y=﹣10x+500求出销售的件数,然后求出政府承担的成本价与出厂价之间的差价;
(2)由利润=销售价﹣成本价,得w=(x﹣10)(﹣10x+500),把函数转化成顶点坐标式,根据二次函数的性质求出最大利润;
(3)令﹣10x2+600x﹣5000=3000,求出x的值,结合图象求出利润的范围,然后设设政府每个月为他承担的总差价为p元,根据一次函数的性质求出总差价的最小值.
试题解析:(1)当x=20时,y=﹣10x+500=﹣10×20+500=300,
300×(12﹣10)=300×2=600元,
即政府这个月为他承担的总差价为600元;
(2)依题意得,w=(x﹣10)(﹣10x+500)
=﹣10x2+600x﹣5000
=﹣10(x﹣30)2+4000
∵a=﹣10<0,∴当x=30时,w有最大值4000元.
即当销售单价定为30元时,每月可获得最大利润4000元;
(3)由题意得:﹣10x2+600x﹣5000=3000,
解得:x1=20,x2=40.
∵a=﹣10<0,抛物线开口向下,
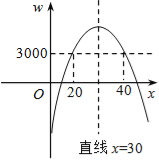
∴结合图象可知:当20≤x≤40时,w≥3000.
又∵x≤25,
∴当20≤x≤25时,w≥3000.
设政府每个月为他承担的总差价为p元,
∴p=(12﹣10)×(﹣10x+500)
=﹣20x+1000.
∵k=﹣20<0.
∴p随x的增大而减小,
∴当x=25时,p有最小值500元.
即销售单价定为25元时,政府每个月为他承担的总差价最少为500元.


科目:初中数学 来源: 题型:
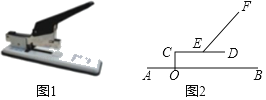
【题目】订书机是由推动器、托板、压形器、底座、定位轴等组成.如图1是一台放置在水平桌面上的大型订书机,将其侧面抽象成如图2所示的几何图形.若压形器EF的端点E固定于定位轴CD的中点处,在使用过程中,点D和点F随压形器及定位轴绕点C旋转,CO⊥AB于点O,CD=12cm连接CF,若∠FED=45°,∠FCD=30°.
(1)求FC的长;
(2)若OC=2cm求在使用过程中,当点D落在底座AB上时,请计算CD与AB的夹角及点F运动的路线之长.(结果精确到0.1cm,参考数据:sin9.6°≈0.17.π≈3.14,![]() 1.732)
1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位需招聘一名技术员,对甲、乙、丙三名候选人进行了笔试和面试两项测试,其成绩如下表所示.根据录用程序,该单位又组织了![]() 名人员对三人进行民主评议,其得票率如扇形图所示,每票
名人员对三人进行民主评议,其得票率如扇形图所示,每票![]() 分(没有弃权票。每人只能投
分(没有弃权票。每人只能投![]() 票)
票)
测试项目 | 测试成绩 | ||
甲 | 乙 | 丙 | |
笔试 |
|
|
|
面试 |
|
|
|
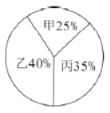
(1)请算出三人的民主评议得分.
(2)该单位将笔试、面试、民主评议三项得分按![]() 确定综合成绩,且民主评议得分低于
确定综合成绩,且民主评议得分低于![]() 分不录取,谁将被录用?请说明理由.
分不录取,谁将被录用?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△P1OA1,△P2A1A2,△P3A2A3,…都是等腰直角三角形,其直角顶点P1(3,3),P2,P3,…均在直线y=﹣![]() x+4上,设△P1OA1,△P2A1A2,△P3A2A3,…的面积分别为S1,S2,S3,…依据图形所反映的规律,S2019=_____.
x+4上,设△P1OA1,△P2A1A2,△P3A2A3,…的面积分别为S1,S2,S3,…依据图形所反映的规律,S2019=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点.已知点A(0,4),点B是x轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当点B的横坐标为4时,m的值是_____.当点B的横坐标为4n(n为正整数)时,m=_____(用含n的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条抛物线与x轴相交于M,N两点(点M在点N的左侧),其顶点P在线段AB上移动,点A,B的坐标分别为(-2,-3),(1,-3),点N的横坐标的最大值为4,则点M的横坐标的最小值为( )

A.-1 B.-3C.-5D.-7
查看答案和解析>>
科目:初中数学 来源: 题型:
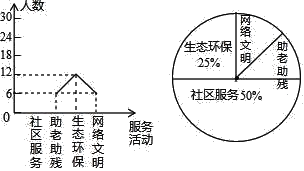
【题目】为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,合肥市某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)请把折线统计图补充完整;
(2)求扇形统计图中,网络文明部分对应的圆心角的度数;
(3)小明和小丽参加了志愿服务活动,请用树状图或列表法求出他们参加同一服务活动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
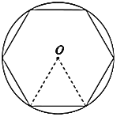
【题目】中国魏晋时期的数学家刘徽首创“割圆术”,奠定了中国圆周率计算在世界上的领先地位.刘徽提出:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”,由此求得圆周率![]() 的近似值.如图,设半径为
的近似值.如图,设半径为![]() 的圆内接正
的圆内接正![]() 边形的周长为
边形的周长为![]() ,圆的直径为
,圆的直径为![]() ,当
,当![]() 时,
时,![]() ,则当
,则当![]() 时,
时,![]() ______.(结果精确到0.01,参考数据:
______.(结果精确到0.01,参考数据:![]() ,
,![]()
![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
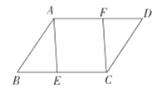
【题目】八年级6班的一个互助学习小组组长收集并整理了组员们讨论如下问题时所需的条件.如图所示,在四边形![]() 中,点
中,点![]() 分别在边
分别在边![]() 上,____________________.求证:四边形
上,____________________.求证:四边形![]() 是平行四边形.你能在横线上填上最少且简捷的条件使结论成立吗?条件分别是:①
是平行四边形.你能在横线上填上最少且简捷的条件使结论成立吗?条件分别是:①![]() ;②
;②![]() ;③
;③![]() ;④四边形
;④四边形![]() 是平行四边形,其中A、B、C、D四位同学所填条件符合题目要求的是( )
是平行四边形,其中A、B、C、D四位同学所填条件符合题目要求的是( )
A.①②B.①②③C.①④D.④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com