
【题目】抛物线y=![]() x2+bx+c经过点A(﹣4,0)、B(2,0)两点,与y轴交于点C,顶点为D,对称轴与x轴交于点H,过点H的直线m交抛物线于P、Q两点,其中点P位于第二象限,点Q在y轴的右侧.
x2+bx+c经过点A(﹣4,0)、B(2,0)两点,与y轴交于点C,顶点为D,对称轴与x轴交于点H,过点H的直线m交抛物线于P、Q两点,其中点P位于第二象限,点Q在y轴的右侧.
(1)求D点坐标;
(2)若∠PBA=![]() ∠OBC,求点P的坐标;
∠OBC,求点P的坐标;
(3)设PQ的中点为M,点N在抛物线上,则以DP为对角线的四边形DMPN能否为菱形?若能,求出点N的坐标;若不能,请说明理由.
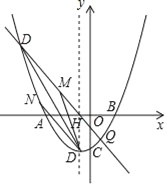
【答案】(1)D(﹣1,﹣3)(2)P(﹣![]() ,
, ![]() );(3)(﹣2
);(3)(﹣2![]() ﹣1,1).
﹣1,1).
【解析】(1)抛物线的解析式为y=![]() (x+4)(x﹣2),然后利用配方法可求得点D的坐标;
(x+4)(x﹣2),然后利用配方法可求得点D的坐标;
(2)在x轴上点E(﹣2,0),连接CE,并延长CE交PB与点F,过点F作FG⊥x轴,垂足为G.首先证明EF=EB=4,然后证明△FGE∽△COE,依据相似三角形的性质可得到FG=![]() ,EG=
,EG=![]() ,故可得到点F的坐标,然后可求得BP的解析式,最后可求得直线与抛物线的交点坐标即可;
,故可得到点F的坐标,然后可求得BP的解析式,最后可求得直线与抛物线的交点坐标即可;
(3)设P(x1,y1)、Q(x2,y2)且过点H(﹣1,0)的直线PQ的解析式为y=kx+b,得到b=k,利用方程组求出点M坐标,求出直线DN解析式,再利用方程组求出点N坐标,列出方程求出k,即可解决问题.
解:(1)∵y=![]() x2+bx+c经过点A(﹣4,0)、B(2,0)两点,
x2+bx+c经过点A(﹣4,0)、B(2,0)两点,
∴y=![]() (x+4)(x﹣2)=
(x+4)(x﹣2)=![]() (x2+2x﹣8)=
(x2+2x﹣8)=![]() (x+1)2﹣3.
(x+1)2﹣3.
∴D(﹣1,﹣3).
(2)如图1,在x轴上点E(﹣2,0),连接CE,并延长CE交PB于点F,过点F作FG⊥x轴,垂足为G.
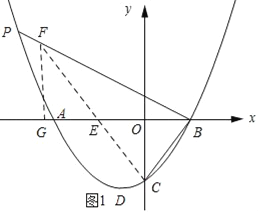
∵点E与点B关于y轴对称,
∴∠OBC=∠OEC.
∴∠OBC=∠GEF.
∵∠PBA=![]() ∠OBC,
∠OBC,
∴∠PBA=∠EFB.∴EF=EB=4.
∵OE=2,OC=![]() ,∴EC=
,∴EC=![]() .
.
∵GF∥OC,∴△FGE∽△COE.
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
解得:FG=![]() ,EG=
,EG=![]() ,
,
∴F(﹣![]() ,
, ![]() ).
).
设BP的解析式为y=kx+b,将点F和点B的坐标代入得: 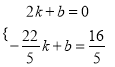 ,
,
解得:k=﹣![]() ,b=1,
,b=1,
∴直线BP的解析式为y=﹣![]() x+1.
x+1.
将y=﹣![]() x+1与y=
x+1与y=![]() x2+
x2+![]() x﹣
x﹣![]() 联立,
联立,
解得:x=﹣![]() ,x=2(舍去),
,x=2(舍去),
∴y=![]() .
.
∴P(﹣![]() ,
, ![]() );
);
(3)设P(x1,y1)、Q(x2,y2)且过点H(﹣1,0)的直线PQ的解析式为y=kx+b,
∴﹣k+b=0,
∴b=k,
∴y=kx+k.
由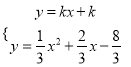 得:
得: ![]() x2+(
x2+(![]() ﹣k)﹣
﹣k)﹣![]() ﹣k=0
﹣k=0
∴x1+x2=﹣2+3k,y1+y2=kx1+k+kx2+k=3k2,
解得:x1=﹣1,x2=3k﹣1,
∵点M是线段PQ的中点,
∴由中点坐标公式的点M(![]() k﹣1,
k﹣1, ![]() k2).
k2).
假设存在这样的N点如图2,
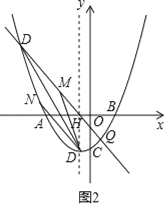
直线DN∥PQ,设直线DN的解析式为y=kx+k﹣3由 ,
,
解得:x1=﹣1,x2=3k﹣1,
∴N(3k﹣1,3k2﹣3).
∵四边形DMPN是菱形,
∴DN=DM,
∴(3k)2+(3k2)2=(![]() )2+
)2+![]() k2+3)2,
k2+3)2,
整理得:3k4﹣k2﹣4=0,
∵k2+1>0,
∴3k2﹣4=0,
解得k=±![]() ,
,
∵k<0,
∴k=﹣![]() ,
,
∴P(﹣3![]() ﹣1,6),M(﹣
﹣1,6),M(﹣![]() ﹣1,2),N(﹣2
﹣1,2),N(﹣2![]() ﹣1,1).
﹣1,1).
∴PM=DN=2![]() ,
,
∵PM∥DN,
∴四边形DMPN是平行四边形,
∵DM=DN,
∴四边形DMPN为菱形,
∴以DP为对角线的四边形DMPN能成为菱形,此时点N的坐标为(﹣2![]() ﹣1,1).
﹣1,1).
“点睛”本题考查二次函数综合题、待定系数法、一次函数、菱形的判定和性质等知识,求得点F的坐标是解答问题(2)的关键,分类讨论是解答问题(3)的关键.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】小王家购买了一套经济适用房,他家准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
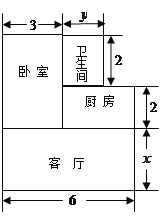
(1)写出用含![]() 、
、![]() 的代数式表示地面总面积;
的代数式表示地面总面积;
(2)已知客厅面积比卫生间面积多21m2,且地面总面积是卫生间面积的15倍,铺1m2地砖的平均费用为80元,求铺地砖的总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2004年6月3日中央新闻报道,为鼓励居民节约用水,北京市将出台新的居民用水收费标准:①若每月每户居民用水不超过4立方米,则按每立方米2元计算;②若每月每户居民用水超过4立方米,则超过部分按每立方米4.5元计算(不超过部分仍按每立方米2元计算).现假设该市某户居民某月用水x立方米,水费为y元,则y与x的函数关系用图象表示正确的是( )
A.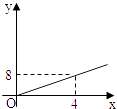
B.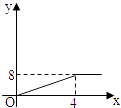
C.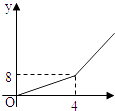
D.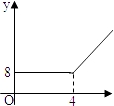
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产A、B两种产品共50件,需购买甲、乙两种材料.生产一件A产品需甲种材料30千克、乙种材料10千克;生产一件B产品需甲、乙两种材料各20千克.经测算,购买甲、乙两种材料各1千克共需资金40元,购买甲种材料2千克和乙种材料3千克共需资金105元.
(1)甲乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过38000元,且生产B产品不少于28件,问符合条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件A产品需加工费200元,生产一件B产品需加工费300元,应选择哪种生产方案,使生产这50件产品的成本最低?(成本=材料费+加工费)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费.月用电量不超过200度时,按0.55元/度计费;月用电量超过200度时,其中的200度仍按0.55元/度计费,超过部分按0.70元/度计费.设每户家庭月用电量为x度时,应交电费y元.
(1)分别求出0≤x≤200和x>200时,y与x的函数表达式;
(2)小明家5月份交纳电费117元,小明家这个月用电多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知线段AB的两个端点分别是A(﹣4,﹣1),B(1,1),将线段AB平移后得到线段A′B′,若点A′的坐标为(﹣2,2),则点B′的坐标为( )
A.(4,3)
B.(3,4)
C.(﹣1,﹣2)
D.(﹣2,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中的真命题是( )
A.在所有连接两点的线中直线最短
B.经过两点有且只有一条直线
C.内错角互补则两直线平行
D.空间中,如果一条直线和两条直线中的一条垂直,那么这条直线也和另一条垂直
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com