
����Ŀ��ij�����ƻ�����A��B���ֲ�Ʒ��50�����蹺��ס������ֲ��ϣ�����һ��A��Ʒ����ֲ���30ǧ�ˡ����ֲ���10ǧ�ˣ�����һ��B��Ʒ��ס������ֲ��ϸ�20ǧ�ˣ������㣬����ס������ֲ��ϸ�1ǧ�˹����ʽ�40Ԫ��������ֲ���2ǧ�˺����ֲ���3ǧ�˹����ʽ�105Ԫ��
��1���������ֲ���ÿǧ�˷ֱ��Ƕ���Ԫ��
��2���ֹ������ڹ���ס������ֲ��ϵ��ʽ���38000Ԫ��������B��Ʒ������28�����ʷ��������������������ļ��֣�
��3���ڣ�2���������£�������һ��A��Ʒ��ӹ���200Ԫ������һ��B��Ʒ��ӹ���300Ԫ��Ӧѡ����������������ʹ������50����Ʒ�ijɱ���ͣ����ɱ�=���Ϸ�+�ӹ��ѣ�
���𰸡�
��1���⣺����Ӳ���ÿǧ��xԪ�����ֲ���ÿǧ��yԪ�����������з�����ã�![]()
��֮![]()
���Ӳ���ÿǧ��15Ԫ�����ֲ���ÿǧ��25Ԫ.
��2��������A��Ʒm��������B��Ʒ��50-m��������������50����Ʒ�IJ��Ϸ�Ϊ15��30m+25��10m+15��20��50-m��+25��20��50-m��=-100m+40000��
�����⣺-100m+40000��38000�����m��20��
�֡�50-m��28�����m��22��
��20��m��22��
��m������
��m��ֵΪ20��21��22��
�������ַ��������±���
A������ | 20 | 21 | 22 |
B������ | 30 | 29 | 28 |
��3�����������ɱ�ΪWԪ���ӹ���Ϊ��200m+300��50-m����
��W=-100m+40000+200m+300��50-m��=-200m+55000��
��W ��m�������������m=20��21��22��
�൱m=22ʱ���ܳɱ���ͣ���ʱW=-200��22+55000=50600Ԫ
����������1�����������ϵ�ǣ����ֲ��ϵĵ���+�����ֲ��ϵĵ���=40�����ֲ��ϵĵ���![]() 2+���ֲ��ϵĵ���
2+���ֲ��ϵĵ���![]() 3=105����δ֪�������������飬�ⷽ������⼴�ɡ�
3=105����δ֪�������������飬�ⷽ������⼴�ɡ�
��2��ץס���йؼ�����֪����������ס������ֲ��ϵ��ʽ��38000������B��Ʒ��������28����δ֪����������ʽ�飬�������ʽ��Ľ⼯��������������⣬�Ϳ������������������������
��3�����������ɱ�ΪWԪ���ӹ���Ϊ��200m+300��50-m�������ݳɱ�=���Ϸ�+�ӹ��ѣ��õ�W��m�ĺ�������ʽ���ٸ���һ�κ��������ʣ����ɵõ���ͳɱ�m��ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͳ�ƾ�4��15�շ������ݣ��������㣬2015��һ����ȫ������������ֵΪ140667��Ԫ����������140667�ÿ�ѧ��������ʾΪ��������
A.1.40667��105
B.1.40667��106
C.14.0667��104
D.0.140667��106
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A=��x��3��2 �� B=��x+2����x��2��
��1���������ʽ2A��B��
��2����2A��B=2����x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̳������ס���������Ʒ��������Ʒÿ������15Ԫ���ۼ�20Ԫ��������Ʒÿ������35Ԫ���ۼ�45Ԫ��
��1�������̳�ͬʱ�����ס���������Ʒ��100��ǡ����ȥ2700Ԫ�����ܹ����ס���������Ʒ�����ټ���
��2�����̳�Ϊʹ�ס���������Ʒ��100�����������������ۼ�![]() ������������750Ԫ���Ҳ�����760Ԫ������������̳������Ӧ�Ľ���������
������������750Ԫ���Ҳ�����760Ԫ������������̳������Ӧ�Ľ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����������У����꼶һ��Ůͬѧ��һ�������������ɼ�����λ���������±���
�ɼ� | 45 | 46 | 47 | 48 | 49 | 50 |
���� | 1 | 2 | 4 | 2 | 5 | 1 |
��˲��Գɼ�����λ���������ֱ�Ϊ�� ��
A.47��49
B.48��49
C.47.5��49
D.48��50
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
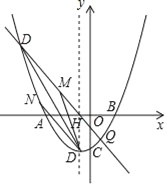
����Ŀ��������y=![]() x2+bx+c������A����4��0����B��2��0�����㣬��y�ύ�ڵ�C������ΪD���Գ�����x�ύ�ڵ�H������H��ֱ��m����������P��Q���㣬���е�Pλ�ڵڶ����ޣ���Q��y����Ҳ࣮
x2+bx+c������A����4��0����B��2��0�����㣬��y�ύ�ڵ�C������ΪD���Գ�����x�ύ�ڵ�H������H��ֱ��m����������P��Q���㣬���е�Pλ�ڵڶ����ޣ���Q��y����Ҳ࣮
��1����D�����ꣻ
��2������PBA=![]() ��OBC�����P�����ꣻ
��OBC�����P�����ꣻ
��3����PQ���е�ΪM����N���������ϣ�����DPΪ�Խ��ߵ��ı���DMPN�ܷ�Ϊ���Σ����ܣ������N�����ꣻ�����ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AD��BC����Ϊ��D��AD��BC���ϵ����ߣ�BE��AC������Ϊ��E��������4�����ۣ���AB=AC���ڡ�EBC= ![]() ����AE=CE���ܡ�EBC=
����AE=CE���ܡ�EBC= ![]() ����ȷ���У� ��
����ȷ���У� ��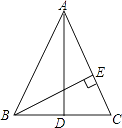
A.�٢�
B.�ڢ�
C.�٢ڢ�
D.�٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������ε����߳��������������������ߵij��ȷֱ�Ϊ3��8�������߳�Ϊ��������ô�����ε��ܳ���__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=ax2+bx+c��a��0����ͼ����x�ύ�ڵ�A����1��0������y��Ľ���B�ڣ�0����2���ͣ�0����1��֮�䣨�����������㣩���Գ���Ϊֱ��x=1�����н��ۣ���abc��0 ��4a+2b+c��0 ��4ac��b2��8a ��![]() ��a��
��a��![]() ��b��c�����к�������ȷ���۵�ѡ���ǣ�������
��b��c�����к�������ȷ���۵�ѡ���ǣ�������

A. �٢� B. �٢ۢ� C. �ڢܢ� D. �٢ۢܢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com